A estrutura é usada para armazenar e desenrolar cabos. A massa combinada da estrutura, do corretel e do cabo é de com centro de massa em . Determine as forças normais nos quatro pés e ) se o cabo sai pela parte de cima do carretel e o cabo sai pela parte de baixo do carretel em seu ponto médio horizontal. O raio efetivo do carretel é de .
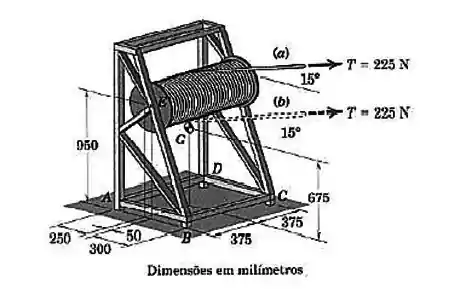
Passo 1
a)
Visto de lado, o negócio fica assim:
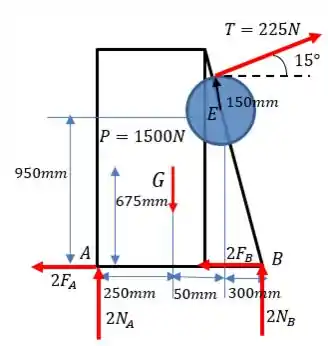
Já que a tensão sempre é aplicada no ponto médio, temos uma simetria que garante que:
E:
Por isso temos e .
Primeiro vamos calcular o binário da força de em relação ao ponto e representar a força de no ponto (o centro do círculo):
Vamos aplicar o equilíbrio de momentos no ponto
Assim:
Agora vamos usar o somatório de forças:
Assim:
Passo 2
b):
E no caso de a força estar assim?
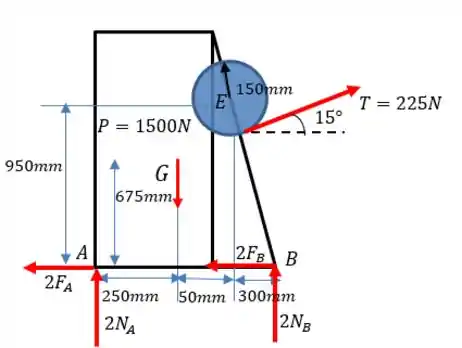
O que vai mudar nesse caso? Apenas o sinal do binário do Assim:
Assim:
Aplicando o equilíbrio de forças:
Assim: