Determine o local e do ponto de aplicação da força de modo que a tração desenvolvida nos cabos , e seja a mesma. Despreze o peso da chapa.
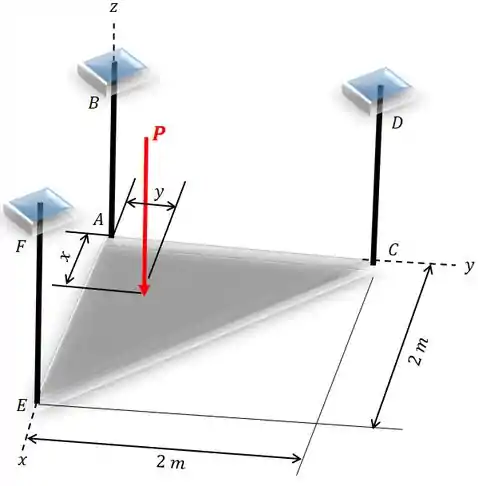
Passo 1
O diagrama de corpo livre fica assim:
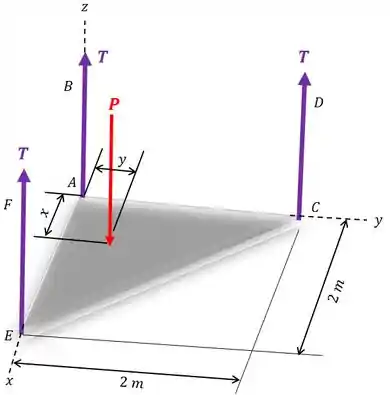
Passo 2
Vamos começar fazendo o equilíbrio de forças verticais:
Vamos deixar esta informação guardada!
Passo 3
Agora vamos calcular o somatório de momentos com relação ao eixo :
Repare que todas as forças que cruzam o eixo não tem braço de alavanca e, portanto, não exercem momento com relação a este eixo!
Sabemos que:
Então, vamos substituir isso na equação do momento:
Cortando , temos:
Passo 4
Agora vamos fazer o somatório de momentos com relação ao eixo :
Já sabemos que:
Então:
Resposta
Exercícios de Livros Relacionados
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B ea tração no membro E D . A força agindo em D é F = 135 i ^
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B e a tração no membro E D . A força agindo em D é F = 135 i
Uma placa circular horizontal de peso igual a 267 N é suspensa por três fios que são ligados a um suporte D e formam ângulos de 30° com a vertical. Determine a tração em cada fio.
Por que as equações escalares de equilíbrio da estática no espaço tridimensional são em número de seis? Mais do que três equações de momento nulo podem ser consideradas nessa equação? Como e por quê?
Determine as forças trativas nos cabos A B , A C e A D .