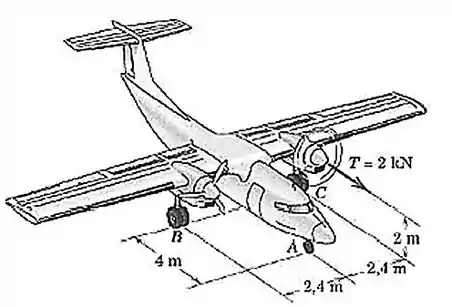
Durante um teste, o motor esquerdo do avião bimotor é acionado gerando um empuxo de . As rodas principais em e estão freadas de modo a evitar movimento. Determine a variação nas forças de reação normais e (comparativamente aos valores nominais com ambos os motores desligados).
Passo 1
A ideia é a seguinte: com os dois motores ligados, havia um grupo de reações que atingiam o avião.
Com apenas uma turbina ligada, essas forças sofrem uma variação. Não queremos achar essas novas forças, mas sim a variação delas. Então, estamos procurando:
Sendo essas as variações das forças normais.
Passo 2
Vamos traçar um eixo que passe por e
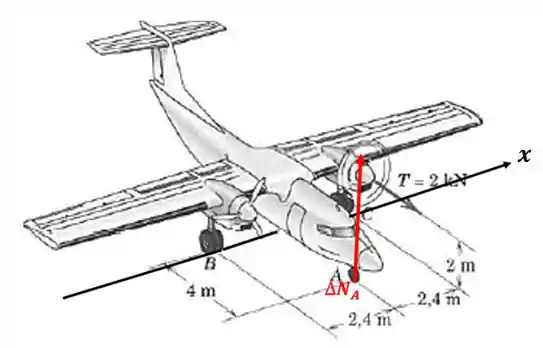
Nesse primeiro momento, queremos descobrir o valor de Desenhando sem o avião e apenas com as forças que nos interessam:
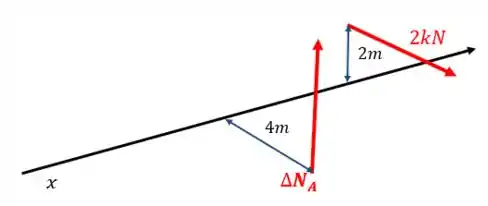
Perceba que elas vão realizar momentos de sentidos contrários.
E qual foi o motivo de não termos usado as outras forças até esse ponto? Bom, porque o eixo passa em cima de e, pontos de aplicação de todas as outras forças. Sendo assim, os momentos delas são nulos ali.
Voltando aos cálculos:
Passo 3
Agora vamos passar um eixo que cruze o ponto
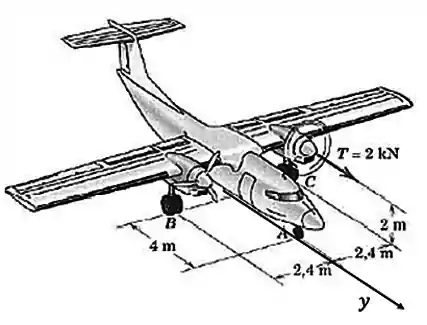
Desenhando sem o avião:
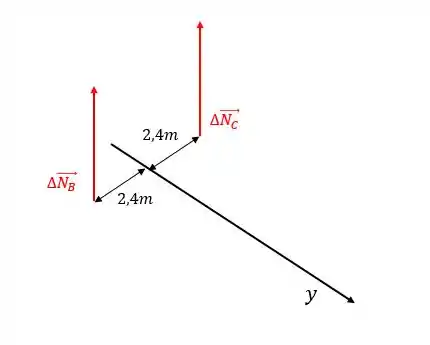
Dá pra perceber que os momentos terão sinais contrários, né? Assim:
Bom, vamos usar essa informa��ão a seguir.
Passo 4
Aí vem uma sacada importante: o que você diria que é o resultado da soma das variações das forças verticais?
Bem, para que o avião fique em equilíbrio, temos que ter:
Ou seja, a soma das forças verticais precisa ser nula. Isso precisa ser respeitado em qualquer condição, mesmo que haja variações.
Sendo assim, a soma das variações das forças precisa ser nula também:
Juntando o que vimos antes: