Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equilíbrio em Três Dimensões

Ver Teoria
Exercício 71234568910111213141516

Enunciado

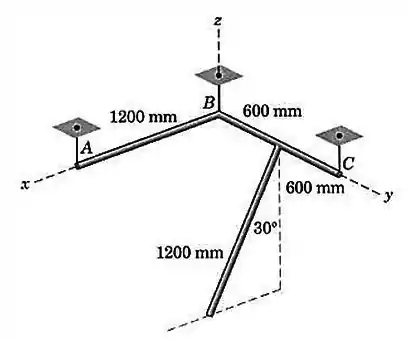
Cada uma das três barras uniformes de 1200   m m tem uma massa de 20   k g . As barras estão soldadas juntas na configuração mostrada e estão suspensas por três arames verticais. As barras A B e B C estão no plano horizontal x y e a terceira barra está em um plano paralelo ao plano x z .Calcule as forças trativas em cada arame.

Passo 1

O diagrama de corpo livre da nossa estrutura fica assim:

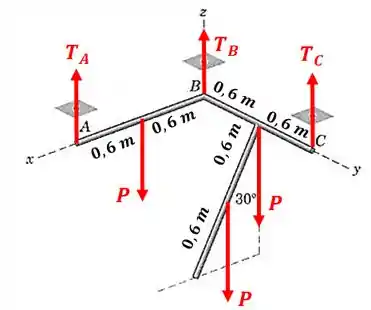
Como todas as barras são uniformes e possuem a mesma massa de 20   k g , a força peso P de todas elas são iguais:

P = 20 9,81       →             P = 196,2   N

Passo 2

Vamos começar calculando o momento com relação ao eixo x , pois duas das nossas incógnitas ( T A e T B ) estão sobre este eixo e, portanto, não vão ter braço de alavanca.

∑ M → x = 0 →

∴

- P 0,6 - P 0,6 + T C 1,2 = 0

∴

- 196,2   0,6 - 196,2   0,6 + T C 1,2 = 0

∴

T C = 196,2   N

Passo 3

Vamos fazer o somatório de momentos com relação ao eixo y agora:

∑ M → y = 0 →

Repare que o braço de alavanca da força peso da barra inclinada será:

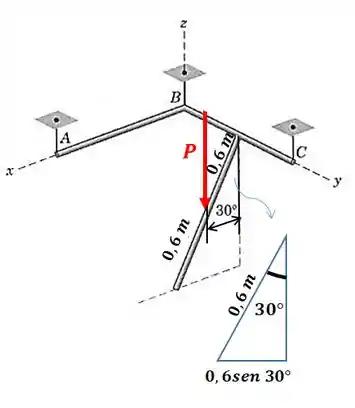
Então:

∑ M → y = 0 →

∴

P 0,6 + P 0,6 s e n   30 ° - T A 1,2 = 0

∴

196,2   0,6 + 196,2   0,3 - T A 1,2 = 0

∴

T A = 147,2   N

Passo 4

Vamos usar o equilíbrio de forças para achar a força que falta:

∑ F → Z = 0 →

∴

T A + T B + T C - P - P - P = 0

∴

147,2 + T B + 196,2 - 196,2 - 196,2 - 196,2 = 0

∴

T B = 245,2   N

Resposta

T A = 147,2   N

T B = 245,2   N

T C = 196,2   N

Exercícios de Livros Relacionados

A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B ea tração no membro E D . A força agindo em D é F = 135 i ^
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B e a tração no membro E D . A força agindo em D é F = 135 i
Uma placa circular horizontal de peso igual a 267 N é suspensa por três fios que são ligados a um suporte D e formam ângulos de 30° com a vertical. Determine a tração em cada fio.
Por que as equações escalares de equilíbrio da estática no espaço tridimensional são em número de seis? Mais do que três equações de momento nulo podem ser consideradas nessa equação? Como e por quê?
Determine as forças trativas nos cabos A B , A C e A D .