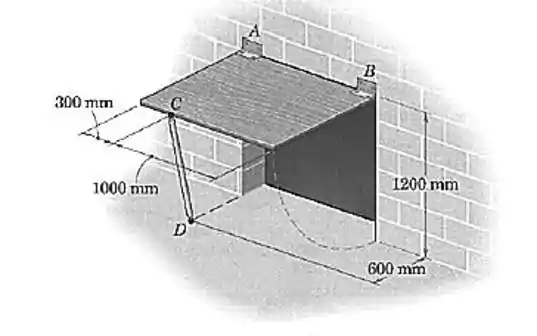
A porta retangular de acesso com é mantida na posição aberta, a , pelo apoio simples . Determine a força no apoio e o módulo da força normal ao eixo de abertura em cada pequena dobradiça e . Considere que na dobradiça a força horizontal e paralela à parede seja nula.
Passo 1
Podemos representar o sistema com o desenho abaixo:
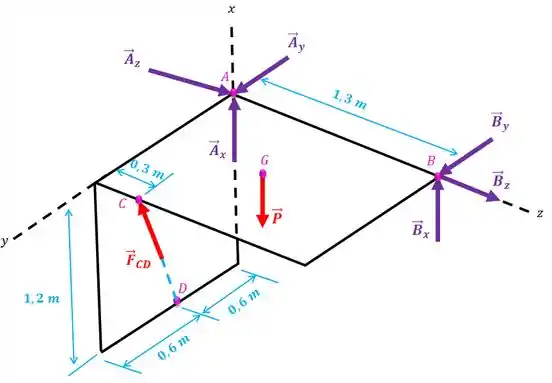
Nós não sabemos quanto vale o módulo da força , mas sabemos calcular a direção dela. Repare que o ponto tem as seguintes coordenadas:
E as coordenadas do ponto são:
Então, a direção é:
Agora temos que transformar isso em um vetor unitário, para isso é só dividirmos pelo seu módulo. Então, vamos começar calculando o módulo:
Então, o vetor unitário vai ser:
Agora sim podemos calcular a nossa força :
Como não sabemos o valor de , vamos deixar assim!
Passo 2
Nosso próximo passo é calcular o módulo da força peso da porta:
Agora que conhecemos todas as forças vamos calcular o momento de cada uma delas com relação aos eixos , e . Vamos escrever a força em termos de suas componentes para facilitar a visualização:
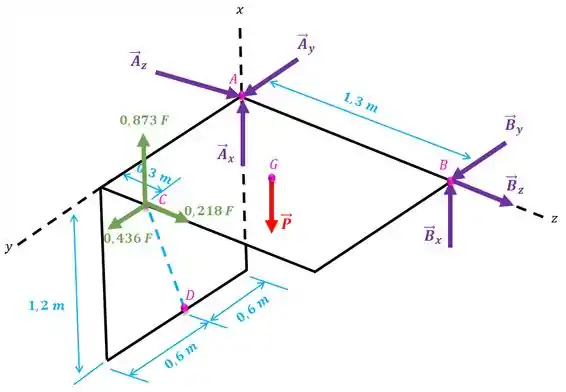
Vamos começar pelo eixo .
Repare que somente o peso e a componente da força exercem momento com relação ao eixo . Isso porque as outras forças não possuem braço de alavanca. Então, vamos lá:
No eixo , a força , o peso e a componente da força possuem braço de alavanca com relação a este eixo:
Como já sabemos o valor do , temos que:
E por último no eixo , as forças que exercem momento são e a componente da força :
Passo 3
Vamos usar o equilíbrio de forças para achar as forças que faltam:
No eixo
No eixo só temos as forças e , então elas vão ser nulas:
O enunciado nos diz para considerarmos a força horizontal e paralela à parede da dobradiça como nula! Essa força que ele tá falando nada mais é do que , assim
Então, a resultante das reações nos pontos e são:
E a força fica: