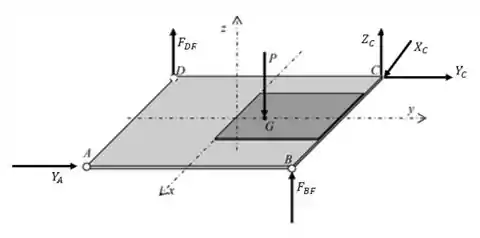
03) A placa quadrada , de lado e densidade superficial , está soldada a uma segunda placa quadrada de lado e densidade superficial . O centro conjunto é apoiado em e e articulado às barras de peso desprezível e , conforme indicado na figura. Sabendo-se que o peso da peça única constituída pelas duas placas homogêneas é e que o seu centro de massa se situa na posição , pede-se:
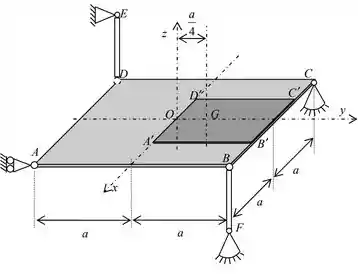
a) Determinar e em função de e dos demais dados fornecidos;
b) Desenhar os diagramas de corpo livre da placa e das barras;
c) Determinar, em função de , as reações nos apoios e e as forças nas barras e .
Passo 1
Fala aí pessoal, tudo tranquilo?
Nessa questão temos uma placa grandona sobre a qual é soldada uma placa menor. O problema é que elas possuem densidades superficiais diferentes, e , respectivamente.
a) Nesse primeiro item, devemos determinar o valor de e . Geralmente, quando temos uma placa homogênea é só fazer:
Onde é a massa da placa e a área superficial. Mas e nesse caso que temos duas placas diferentes, o que dá pra ser feito?

Então, a ideia é fazer um ajuste nas equações. Tipo, a massa total das placas, por exemplo, é dada por:
é a massa da placa maior, e pode ser calculado como uma placa homogênea normal, daí:
Analogamente para a placa menor:
No enunciado, a massa total é dada através do Peso.
Outra equação que podemos usar é a do centro de massa. Sabemos que, em por exemplo, a posição do centro de massa é dada por:
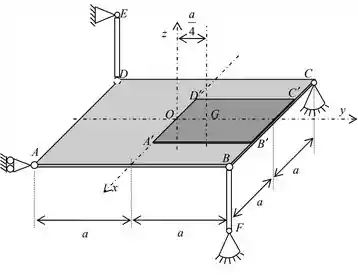
está bem no centro da placa grande, ou seja, na origem. Já está no meio da placa menor, ou seja, no meio do quadrado , assim .
Escrevendo a equação, e sabendo que pelo enunciado , temos:
Daí, vem que:
Logo, pela equação :
Prontinho! 😉
Passo 2
b) Nesse item precisamos desenhar o diagrama de corpo livre (DCL) das barras e do conjunto de placas soldadas.
Começando pelas barras, ambas estão sendo tracionadas (ou comprimidas) ao longo do seu eixo, de modo que podemos desenhar:

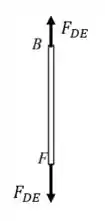
Já para a estrutura das placas, temos basicamente a força peso atuando no seu centro de massa, e as reações dos nós e . Daí:
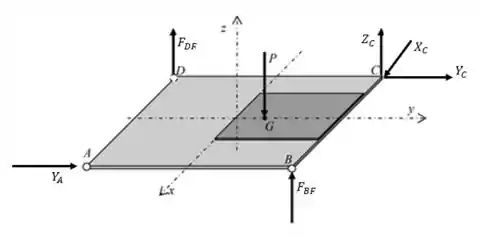
Passo 3
c) Aqui a questão nos pede para encontrar as reações nos apoios e e as forças nas barras e .
A ideia é escrever as equações de equilíbrio da placa, em e . Além das equações dos momentos, que também são nulos. Assim, olhando para o DCL da placa, temos:
Ainda precisamos de mais equações, pois temos variáveis. Daí:
De , vem que:
Substituindo esse resultado em , temos:
De , temos:
Substituindo esse resultado em , temos:
Massa! Substituindo ambos resultados em , temos:
Pra finalizar mais uma questãozinha, é só encontrar :
Onde os sentidos propostos inicialmente estavam corretos 😊
Prontinho, galera! Matamos mais uma questão.
Espero vocês na próxima, tamo junto 😊
Resposta
a)
b) Resolução no texto.
c) Resolução no texto.