A parte de um lustre que é sustentada por correntes tem a forma de uma parte de casca esférica. Se a massa da parte de vidro é , determine a força trativa em cada uma da correntes.
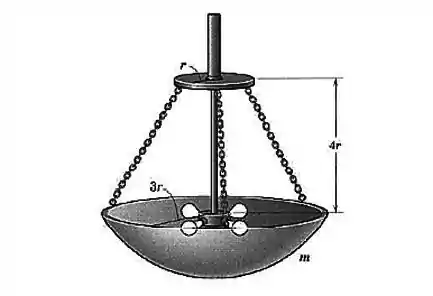
Passo 1
Bom, quais são as forças que agem no sistema?
A força peso e a força de tensão em cada uma das correntes.
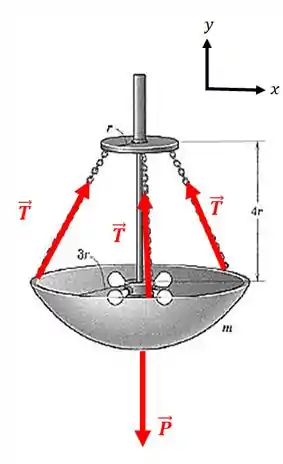
Para que a massa esteja em equilíbrio, vamos precisar garantir que:
Passo 2
O sistema simplificado pode ser representado assim:
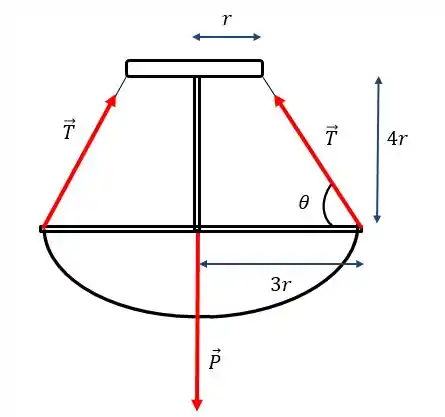
Passo 3
Bom, pelo desenho e pelo enunciado, percebemos que as componentes verticais das tensões () vão equilibrar o peso. Assim, podemos escrever:
Lembre-se: são três correntes igualmente espaçadas, sendo assim, são três tensões.
Passo 4
Pelo triângulo formado pela tensão, podemos dizer:
Nós só não sabemos quem é mas basta usarmos o triângulo retângulo da figura:
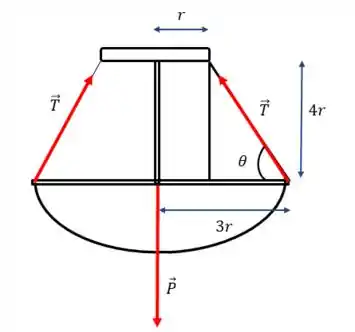
Pra ficar mais fácil de ver, vamos tirar o triângulo do desenho:
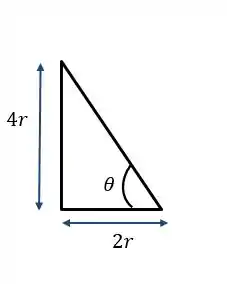
Assim:
Passo 5
Então: