Um bloco de é unido a uma mola e colocado em uma superfície horizontal sem atrito. Uma força horizontal de é necessária para manter o bloco em repouso quando é puxado de de sua posição de equilíbrio. O bloco é liberado do repouso a partir deste ponto e realiza um movimento harmônico simples.

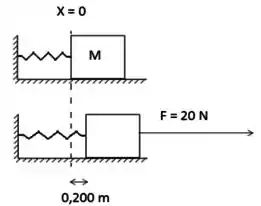
1. Encontre a constante de força da mola e a frequência de oscilação.
2. Determine a energia cinética máxima do bloco.
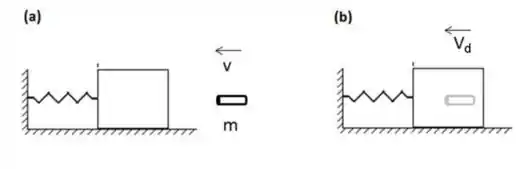
3. Considere agora que o bloco esteja em repouso na sua posição de equilíbrio e um projétil de massa com velocidade de atinge o bloco, como mostra a figura (a) abaixo. O projétil fica preso no bloco, como mostrado na figura (b), e o sistema bloco+projétil passa a oscilar num movimento harmônico simples. Determine a amplitude do MHS resultante.



4. Se o projétil do item c) atingir o bloco quando este se encontra com velocidade nula na posição , qual será a nova amplitude do movimento?

a)

Aqui queremos encontrar a constante de força da mola e a frequência de oscilação.

O enunciado te deu o da mola e a força gerada por ela, então, para calcular a constante:

E a frequência angular é dada por:

A frequência de oscilação será:

b)

A energia cinética máxima ocorre quando toda a energia mecânica é cinética. Ou seja:

E a energia mecânica máxima é dada por:

Onde é a amplitude do movimento.

E qual a amplitude do movimento? Nesse caso, vale:

Então:

Então:

c)

Bom, galera, aqui vamos lembrar um pouco do que sabemos sobre colisões.

Como o sistema é isolado de forças externas, podemos dizer que o momento se conserva e então:

Então:

Essa é a velocidade do conjunto corpo mais bloco.

Beleza, mas e aí? Não queremos isso. Queremos saber é qual a amplitude do MHS.

Basta a gente lembrar que a energia cinética máxima é igual a , então:

Calculando

Então, usando a equação anterior:

d)

Após o choque, a velocidade continua a mesma que a do item c), só que agora temos também energia potencial. Então: