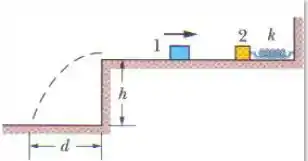
A figura abaixo mostra o bloco 1, de massa , deslizando para a direta, sobre uma superfície elevada, com uma velocidade de s. O bloco sofre uma colisão elástica com o bloco 2, inicialmente em repouso, que está preso a uma mola de constante elástica (Suponha que a mola não afete a colisão.) Após a colisão, o bloco 2 inicia um MHS com um período de e o bloco 1 desliza para fora da extremidade oposta da superfície elevada, indo cair a uma distância horizontal de dessa superfície, depois de descer uma distância de . Qual é o valor de ?
Passo 1
Bom, primeiro vamos dar uma resumida nesse enunciado aí! =p
De início, temos uma colisão elástica entre as massas 1 e 2, ambas sobre a superfície elevada. Depois disso, a massa 2 entra em MHS, enquanto a massa 1 cai da superfície elevada, percorrendo uma distancia horizontal , que é o que queremos achar.
Passo 2
Como o enunciado disse que a mola não afeta a colisão, nós podemos usar as fórmulas que nos dão as velocidades em uma colisão elástica.
Porém, antes disso, vamos achar a massa do bloco 2.
Como temos a frequência com que ele oscila após a colisão a e constante da mola, podemos fazer:
Só basta a gente calcular
Assim:
Passo 3
Agora vamos escrever a equação da conservação do momento pra essa colisão:
Além dessa, temos a equação da conservação da energia:
Show?? Temos duas incógnitas ali: (velocidades dos blocos após a colisão).
Vamos resolver o sistema acima, isolando na primeira equação e substituindo na segunda
Assim, na segunda equação fica
Agora, vamos fazer as contas e achar . Podemos já substituir e os valores das massas, também.
Abrindo esse produto notável
Chegando na equação
Temos as duas raízes e . Mas se valesse , isso implicaria que o bloco teria uma velocidade nula, o que sabemos, pelo enunciado, que não é verdade.
Excluindo a raiz negativa, encontramos pra
Passo 4
Agora é só cinemática!!!! Essa velocidade, , vai ser a velocidade do bloquinho 1 após a colisão. Como ele vai cair da mesa, essa vai ser a velocidade inicial do lançamento oblíquo.
Então, pra achar o alcance, vamos usar:
Onde é o tempo de queda. E como se calcula ele mesmo? Lembrando das fórmulas de lançamento oblíquo, a gente pode escrever:
Aplicando o valor da altura do enunciado:
Assim: