Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de MHS + Colisões

Ver Teoria
Exercício 412356789101112

Enunciado

Imagine um experimento em que temos um carrinho de massa m A , inicialmente em repouso, preso a uma mola relaxada de constante elástica k e que pode se deslocar sem atrito sobre uma mesa horizontal. Nesse experimento, um carrinho de massa m B se aproxima com uma velocidade v B e colide frontalmente com o primeiro carrinho. Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos.

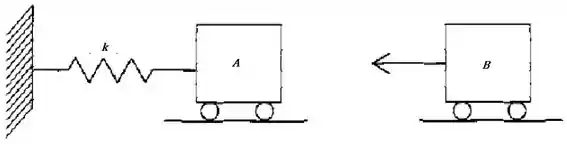
Calcule a velocidade v D dos blocos logo após a colisão, a frequência angular ω de oscilação e a amplitude, A , do movimento.

Passo 1

Bom, num primeiro momento a gente precisa se lembrar de um conceito lááá de Física 1...Lembra da conservação de momento linear? O quêêê??? Não se lembra??? Td bem, o Responde Aí está aqui pra isso

Se nós voltarmos lá nos nossos assuntos de Conservação do Momento Linear e de Colisões, vamos ver que:

Q t d . m o v . a n t e s = Q t d . m o v . d e p o i s

∴

m B v B = m A v D + m B v D   → v D = m B v B m A + m B

Passo 2

Para calcularmos a frequência angular de oscilação, basta nos lembrarmos que

ω = k M

Reparou no M ali? Ele será a soma das massas dos dois carrinhos, ou seja, M = m A + m B . Aí ficou fácil, né?

ω = k M = k m A + m B

Show de bolinhas! Agora só falta calcular a Amplitude!!!

Bom...nós vamos matar isso por energia.

Nós temos a velocidade máxima dos blocos, pois é aquela que eles têm logo após o impacto.

Então temos a energia cinética máxima. Basta a gente descobrir qual é a energia potencial máxima para descobrirmos a amplitude, pois:

E P m á x = k A 2 2

E a energia cinética é:

E c m á x = m v m á x 2 2 = m A + m B . m B v B m A + m B 2 . 1 2 = m B 2 v B 2 2 m A + m B

E isso é igual a :

k A 2 2 = m B 2 v B 2 2 m A + m B

∴

A = m B v B . 1 k m A + m B

Resposta

v D = m B v B m A + m B

A = m B v B . 1 k m A + m B

ω = k m A + m B

Exercícios de Livros Relacionados

Na figura, o bloco 2 , de massa 2,0k g , oscila na extremidade de uma mola em MHS com um período de 20m s . A posição do bloco é dada por x = 1,0c m c o s ⁡ ( ω t + π / 2 ) . O bloco 1 , de massa 4,0k
Um bloco que desliza em uma superfície horizontal sem atrito está preso a uma mola horizontal de constante elástica 600N / m . O bloco executa um MHS em torno da posição de equilíbrio com um período d
69. Uma massa de 10k g está se deslocando para direita com uma velocidade igual a 2,0m / s sobre uma superfície horizontal quando colide com uma segunda massa inicialmente em repouso, mas presa a uma
Um bloco de 4,00 k g está suspenso por uma mola com k = 500 N / m . Uma bala de 50,0 g é disparada verticalmente contra o bloco, de baixo para cima, com uma velocidade de 150 m / s , e fica alojada no