Um carrinho de massa , inicialmente em repouso no ponto , está preso a uma mola relaxada de constante elástica e pode se deslocar sem atrito sobre uma mesa horizontal. Um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o carrinho . Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos. Encontre, em função dos dados acima,
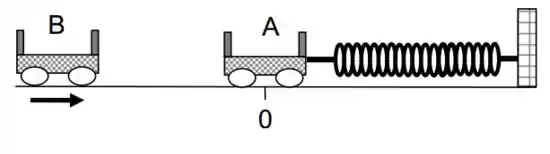
- A velocidade dos blocos logo após a colisão.
- A frequência angular de oscilação e a amplitude, , do movimento.
- Considerando o instante de choque, obtenha a constante de fase e escreva a posição em função do tempo,
- Suponha que ao atingir a posição o carrinho se solte do sistema. Encontre a nova velocidade do carrinho ao passar pelo ponto
Passo 1
a)
Bem, aqui a gente só precisa lembrar da conservação de momento linear em colisões. Se tiver alguma dúvida, dê uma olhada lá no nosso guia de colisões.
Passo 2
b)
Vamos precisar também lembrar dos conceitos de energia. Nós temos a velocidade máxima dos blocos, pois é aquela que eles têm logo após o impacto.
Então temos a energia cinética máxima. Sabemos que essa energia cinética máxima é igual à energia potencial máxima:
E a energia cinética é:
Assim:
E a frequência angular é facilmente achada usando-se a fórmula:
Passo 3
c)
A função é a função que nos dá a posição de um MHS, então ela tema a forma:
Temos todas as informações, menos a . Só que pelo enunciado, em , . Então:
Ou seja, um múltiplo ímpar de
Vamos analisar o sinal da velocidade em pra saber mais da constante de fase:
Em
ou
Então:
Ou
Com e dados na letra b.
Passo 4
d)
Quando o carrinho se solta em , a energia mecânica se conserva.
Isso quer dizer que vamos ter que calcular a energia mecânica naquele ponto e depois calcular ela no ponto , onde a velocidade é máxima. Assim, lembrando que a massa do sistema diminuiu, podemos escrever:
Então:
Resposta
a)
b)
c)
d)