Considere dois pêndulos simples, de mesmo comprimento l, presos a um mesmo ponto como mostra a figura. A partícula de massa é solta do repouso a uma altura z em relação à posição de equilíbrio e atinge a partícula de massa em t = 0 s. Anteriormente, a partícula de massa estava em repouso, na posição de equilíbrio. Após a colisão as duas partículas permanecem juntas.
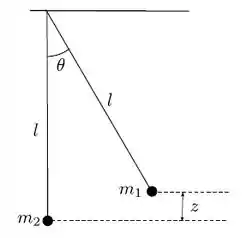
Considerando que a aceleração da gravidade g é conhecida e que, tanto antes quanto depois da colisão, vale a aproximação de pequenos ângulos para ambos os pêndulos, a amplitude do movimento pode ser escrita como:
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiro vamos achar a velocidade da massa 1 logo antes do choque. Vamos fazer conservação de energia mecânica!
Passo 2
Agora vamos achar a velocidade das duas massas depois do choque. Vamos usar conservação do momento linear!
Passo 3
Você lembra que no pêndulo simples:
E no MHS:
Então no pêndulo simples:
Por que eu to te dizendo isso? Porque isso vai nos ajudar a relacionar a energia mecânica com a frequência angular do pêndulo simples!
Lembra que no MHS a energia mecânica é constante? Essa constante é:
Mas aqui, como nossos deslocamentos são angulares e não lineares, teremos que usar ângulos! Então:
E vamos trocar k pelo que achamos antes:
Passo 4
Show! Logo após o choque, quando as massas estiverem na velocidade que a gente calculou a velocidade vai ser máxima! Porque a energia potencial vai ser mínima. Então na velocidade a energia cinética vai ser igual a energia mecânica!
Só que aqui, como a gente tem ângulos, vamos usar uma fórmula diferente pra energia cinética. Vai ser:
Porque em vez da velocidade v a gente tá usando a velocidade ANGULAR, que é .
Vamos igualar:
Passo 5
Vamos trocar o valor de :
Resposta
Letra C.