Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 2134567891011121314

Enunciado

Encontre o momento de inércia em relação ao eixo x de uma placa fina limitada pelas curvas x = y 2 e x = 2 y - y 2 se a densidade no ponto ( x , y ) for δ x , y = y + 1 .

Passo 1

A gente viu na teoria que o momento de inércia em relação ao eixo x pode ser encontrado pela fórmula:

I x = ∬ D   y 2   δ ( x , y ) d A

Então só temos que ver como que vai ficar a região para podermos resolver a integral.

Passo 2

A nossa região vai ser o interior da interseção de duas parábolas, que podemos esboçar assim:

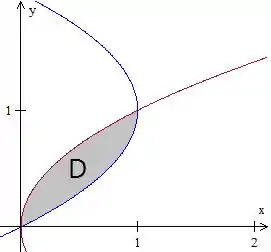
Que podemos escrever tanto como tipo 1 , quanto tipo 2 , mas vamos escolher o tipo 2 porque tem equações mais simpáticas pros limites do x .

Dessa forma, vamos ter y variando entre 0 e aquele ponto de interseção entre as parábolas, dado em:

y 2 = 2 y - y 2 → 2 y 2 = 2 y

y 1 = 0           y 2 = 1

Então nossa região vai ser descrita por:

D = ( x , y ) ∈ R 2 | 0 ≤ y ≤ 1 , y 2 ≤ x ≤ 2 y - y 2

Agora é só calcular a integral!

Passo 3

Tinhamos a fórmula:

I x = ∬ D   y 2   δ x , y d A

⇒ ∫ 0 1 ∫ y 2 2 y - y 2 y 2 y + 1 d x d y

⇒ ∫ 0 1 ( y 3 + y 2 ) ∙ x │ y 2 2 y - y 2 d y = ∫ 0 2 ( y 3 + y 2 ) ∙ 2 y - y 2 - y 2 d y

= ∫ 0 1 ( y 3 + y 2 ) ∙ 2 y - 2 y 2 d y = ∫ 0 1 2 y 4 - 2 y 5 + 2 y 3 - 2 y 4   d y = ∫ 0 1 - 2 y 5 + 2 y 3   d y

⇒ - y 6 3 │ 0 1 + y 4 2 │ 0 1 = - 1 3 + 1 2 = - 1 ∙ 2 + 1 ∙ 3 6

⇒ 1 6

Resposta

I x = 1 6

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K