Uma lâmina homogênea tem a forma de um triângulo equilátero de lado . Ache o momento de inércia em relação a um lado.
Passo 1
Momento de inércia em regiões planas vai ser sempre alguma dessas fórmulas aqui:
Mas vamos ver qual vamos escolher pra esse triângulo aí.
Passo 2
Podemos desenhar ele no plano assim:
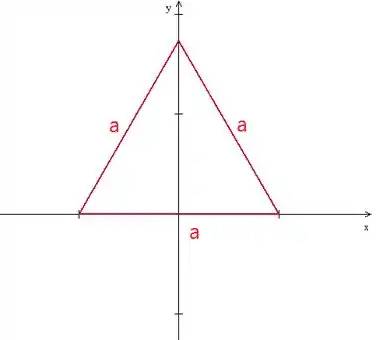
Então o momento de inércia a um lado pode ser o momento de inércia em relação a base, que está no eixo .
E ele diz que a lâmina é homogênea, o que é o mesmo que dizer que a densidade é constante.
A fórmula que vamos usar, então, vai ser:
Passo 3
A região é do tipo e a altura do triângulo equilátero é dada por:
Então vamos ter e variando entre as duas retas dos lados do triângulo, que vão ter equações:
Então nossa integral vai ser:
E, apesar de super esquisito, é só calcularmos.
Passo 4
Os valores são feiões, mas a conta não é difícil:
Ufa, foi! As contas foram estranhas, mas é só a gente deixar tudo organizadinho e não se perder que não fica tão difícil assim.