Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 4123567891011121314

Enunciado

Seja uma lâmina delgada representada pela região D , determinada por y ≤ x , y ≥ - x , x 2 + y 2 ≥ 2 x e x 2 + y 2 ≤ 4 x . Se a densidade em cada ponto é dada por ρ x , y = 1 x 2 + y 2 , determine o momento de inércia em relação à origem.

Passo 1

Antes de qualquer coisa vamos determinar a figura que mostra D

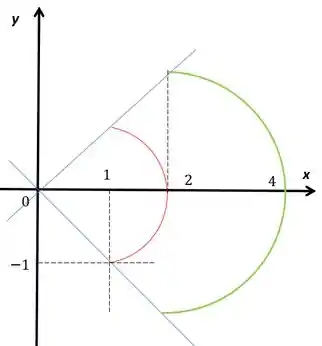
A área vai ser entre as circunferências limitados pelas retas azuis.

Passo 2

Como tanto a função que vamos integrar como a região de integração possuem termos x 2 e y 2 , vamos utilizar coordenadas polares. Faremos, então:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Passo 3

Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.

Repara que o ângulo θ vai variar de um extremo da circunferência até o outro. Olha o desenho com o ângulo marcado

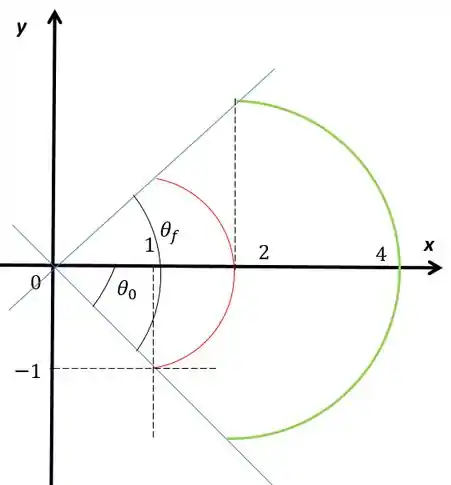
Então

θ 0 = - π 4

θ f = π 4

Vamos ver agora o valor de r . Pelas equações das circunferências temos

2 x ≤ x 2 + y 2 ≤ 4 x

Vamos trocar pelas coordenadas polares

2 r cos ⁡ θ ≤ r cos ⁡ θ 2 + r sen ⁡ θ 2 ≤ 4 r cos ⁡ θ

2 r cos ⁡ θ ≤ r 2 cos ⁡ θ 2 + sen ⁡ θ 2 ≤ 4 r cos ⁡ θ

2 r cos ⁡ θ ≤ r 2 ≤ 4 r cos ⁡ θ

Como r > 0

2 cos ⁡ θ ≤ r ≤ 4 cos ⁡ θ

Vamos ter

D = { ( r , θ ) | 2 cos ⁡ θ ≤ r ≤ 4 cos ⁡ θ ; -   π / 4 ≤ θ ≤ π / 4 }

Passo 4

O momento de inércia vai ser

I = ∬ D x 2 + y 2 ρ x , y d x d y = ∬ D x 2 + y 2 x 2 + y 2 d x d y = ∬ D x 2 + y 2 d x d y

Em coordenadas polares vamos ter

M = ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r cos ⁡ θ 2 + r sen ⁡ θ 2 d r d θ

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r 2 cos ⁡ θ 2 + sen ⁡ θ 2 d r d θ =

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r r 2 d r d θ =

= ∫ - π / 4 π / 4 ∫ 2 cos ⁡ θ 4 cos ⁡ θ r 2 d r d θ = ∫ - π / 4 π / 4 r 3 3 r = 2 sen ⁡ θ r = 4 cos ⁡ θ d θ = ∫ - π / 4 π / 4 4 cos ⁡ θ 3 3 - 2 cos ⁡ θ 3 3 d θ =

∫ - π / 4 π / 4 64 cos 3 ⁡ θ 3 - 8 cos 3 ⁡ θ 3 d θ = ∫ - π / 4 π / 4 56 cos 3 ⁡ θ 3 d θ = 56 3 ∫ - π / 4 π / 4 cos 3 ⁡ θ d θ

Vamos fazer essa integral separada,

Passo 5

∫ cos 3 ⁡ θ d θ = ∫ cos 2 ⁡ θ cos ⁡ θ d θ = ∫ 1 - sen 2 ⁡ θ cos ⁡ θ d θ

Agora fazemos

sen ⁡ θ = u

d u = cos ⁡ θ d θ

A integral vai ficar

∫ 1 - sen 2 ⁡ θ cos ⁡ θ d θ = ∫ 1 - u 2 d u

Resolvendo a integral temos

∫ 1 - u 2 d u = u - u 3 3

Voltando para θ

u - u 3 3 = sen ⁡ θ - s e n 3 θ 3

Passo 6

Voltando para a integral que tínhamos, vamos ter

56 3 ∫ - π / 4 π / 4 cos 3 ⁡ θ d θ = 56 3 sen ⁡ θ - s e n 3 θ   3 θ = - π / 4 θ = π / 4

= 56 3 sen ⁡ π 4 - sen 3 ⁡ π 4 3 - sen ⁡ - π 4 - sen 3 ⁡ - π 4 3

= 56 3 2 2 - 2 2 3 3 - - 2 2 - - 2 2 3 3

= 56 3 2 2 - 2 2 8 3 - - 2 2 - - 2 2 8 3

= 56 3 2 2 - 2 12 - - 2 2 + 2 12

= 56 3 5 2 12 - - 5 2 12

= 56 3 10 2 12

= 56 3 5 2 6

= 280 2 18

= 140 2 9

Resposta

140 2 9

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K