Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 1412345678910111213

Enunciado

  1. Uma lâmina homogênea tem a forma de um triângulo equilátero de lado a . Ache o momento de inércia em relação
  1. A uma altura

Passo 1

Primeira coisa... Sim! Desenho desse triângulo no plano hehe!

Mas cara, como queremos o momento de inércia em relação a uma altura, nada mais justo que façamos esse triângulo exatamente com altura coincidindo com um dos eixos, certo?

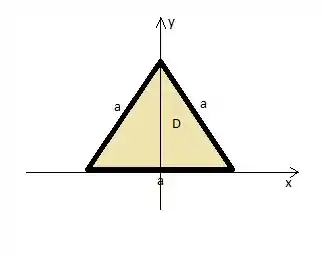
No caso que vamos pegar, coincide com o eixo y mesmo, como você pôde notar.

Passo 2

Momento de inércia em relação ao eixo y é...

I y = ∬ D x 2 ρ x ,   y   d A

Esse ρ x ,   y é a densidade da região, mas como essa região é homogênea, a função de densidade é uma constante k , logo podemos eliminá-la da integral:

I y = k ∬ D x 2   d A

Bem, para resolver essa integral dupla, vem comigo no processo para descrever a região D , o triângulo.

Passo 3

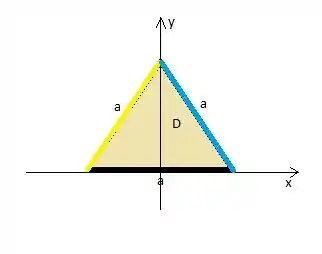
Você e eu podemos classificar a região D é como do tipo 2 e a altura do triângulo equilátero é dada por:

h = l 2 3 = a 3 2

Então vamos ter o y variando de 0 até a o valor da altura

0 ≤ y ≤ a 3 2

e x variando entre as duas retas dos lados do triângulo,

R e t a   a m a r e l a ≤ x ≤ R e t a   a z u l

Bora buscar a equação dessas retas aí então!

Passo 4

A reta amarela passa por dois pontos: ela sai do ponto - a 2 , 0 e vai até o ponto 0 , a 3 2 . Vamos recordar, aqui, como encontrar uma reta com dois pontos e o que devemos fazer primeiro é calcular o ∆ y

∆ y = a 3 2 - 0 = a 3 2

e ∆ x = 0 - - a 2 = a 2

colocando na forma geral de reta

y - y 0 = ∆ y ∆ x x - x 0

e substituindo ( x 0 ,   y 0 ) pela coordenada do pondo de chegada, ou seja

( x 0 ,   y 0 ) = 0 , a 3 2

y - a 3 2 = a 3 2 a 2 x                 ⇒ a r r u m a n d o   d e   u m a   f o r m a   m a i s b e l a           y = 3 x + a 3 2

Como queremos R e t a   A m a r e l a ≤ x ≤ R e t a   a z u l

basta isolarmos o x em função do y , ali

          y - a 3 2 = 3 x             ⇒                 x = y 3 - a 2

logo...

y 3 - a 2 ≤ x ≤ R e t a   a z u l

Quanto à reta azul, bem! Ela é a mesma reta, só que decrescente

y = - 3 x + a 3 2     ⇒ x = - y 3 + a 2

y 3 - a 2 ≤ x ≤ - y 3 + a 2

Passo 5

Com esses dados em mãos, retornemos à integral dupla que queremos resolver...

I y = k ∬ D x 2   d A =

∫ 0 a 3 2 ∫ y 3 - a 2 - y 3 + a 2 x 2 d x d y

Os valores são feiões, mas a conta não é difícil:

k ∫ 0 a 3 2 ∫ y 3 - a 2 - y 3 + a 2 x 2 d x d y =

k ∫ 0 a 3 2 x 3 3 y 3 - a 2 - y 3 + a 2 d y =

k ∫ 0 a 3 2 - y 3 + a 2 3 3 - y 3 - a 2 3 3 d y

Olha só que interessante! Resolver essas duas diferenças de cubos ali, complicaria muito, certo? Porém, aquele menos que está na frente do segundo termo - y 3 - a 2 3 3 , pode passar pra dentro, afinal - 1 3 = - 1 3

k ∫ 0 a 3 2 - y 3 + a 2 3 3 + - 1 y 3 - a 2 3 3 d y =

k ∫ 0 a 3 2 - y 3 + a 2 3 3 + - y 3 + a 2 3 3 d y =

Legal, neh? agora

k ∫ 0 a 3 2 2 ∙ - y 3 + a 2 3 3 d y =

k 2 3 ∫ 0 a 3 2 - y 3 + a 2 3 d y =

Fazendo uma substituição simples, obtemos

- y 3 + a 2 = t         ⇒       d t = - 1 3 d y        

⇒       d y = - 3   d t

Agora não se esqueça de substituir também os termos dos limites...

y = 0                 →                   t = a 2

y =   a 3 2               →                   t = - a 2 + a 2 = 0

Jogando todo na integral

k 2 3 ∫ 0 a 3 2 - y 3 + a 2 3 d y = k 2 3 ∫ a 2 0 t 3 - 3   d t =

- k 2 3 3 t 4 4 a 2 0 =

substituindo e simplificando ganhamos...

0 - - k 2 3 3 a 2 4 4 =

o resultado

k 3 a 4 96

Resposta

k 3 a 4 96

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K