Uma placa fina de densidade constante tem a forma de um setor circular de raio e ângulo central . Mostre que o momento de inércia em relação à bissetriz do ângulo é dado por
Onde é a massa da placa.
Passo 1
Bem, como ele pede momento de inércia a gente sabe que com certeza vamos usar alguma dessas fórmulas:
Mas vamos tentar entender como que é essa placa pra sabermos como fazer isso direito.
Passo 2
Se desenharmos essa tal placa no plano vamos ter alguma coisa desse tipo aqui, olha:
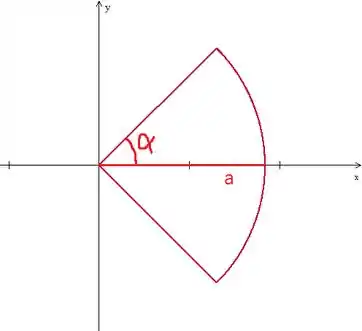
Ou seja, a bissetriz vai ser exatamente o eixo , e vamos utilizar essa fórmula:
Já que ele diz que a densidade é constante.
Só que a gente vê pelo desenho que seria muito melhor descrever a região por coordenadas polares, então vamos ver como que vai ficar!
Passo 3
Vamos lembrar como que é a mudança pra coordenadas polares:
Então a vamos ter:
Mas agora o domínio de é tranquilo de ser escrito em coordenadas polares, porque temos simplesmente:
Então a gente fica com:
Bem, a gente resolveu tudo, agora vamos tentar dar uma mnipulada nisso até chegarmos no resultado que ele pediu...
Passo 4
Primeiro, vamos lembrar que , então vamos ter:
Agora é so lembrar que a área do setor circular é:
E que massa vai ser o produto da densidadecom a área:
Então vamos multiplicar aquele no numerador e no denominador por e vamos ter:
E pronto, finalmente chegamos lá! Essas questões de “mostre” são sempre chatinhas, hein?
Resposta
Ei, a resposta está no passo a passo :)