Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 6123457891011121314

Enunciado

Uma placa fina é limitada pela circunferência x 2 + y 2 = a 2 , a > 0 , e tem densidade ρ x ,   y = a 2 a 2 + x 2 + y 2 . Calcule o momento de inércia polar em função de sua massa M .

Passo 1

Eu ouvi momento de inércia polar? Cara! Aplica a fórmula:

I p = ∬ D x 2 + y 2 ∙ ρ x ,   y   d A

como a função de densidade foi dada, basta que apliquemos a integral:

∬ D x 2 + y 2 ∙   a 2 a 2 + x 2 + y 2 d A

Agora, precisamos saber quem é essa região D aí. Bora?

Passo 2

A região D é limitada por uma circunferência de raio a :

x 2 + y 2 = a 2

que geometricamente nos representa

Pow! Repare que estamos trabalhando com uma região circular

e com coisas ao quadrado se somando. Então são muito úteis as coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

além disso, uma equação linda que nos ajuda é a equação da circunferência:

x 2 + y 2 = r 2

Passo 3

Não podemos deixar de encontrar os limites das novas variáveis:

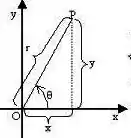
Observando então quem é θ e r e comparando com a nossa região...

Teremos o ângulo dando uma volta completa

0 ≤ θ ≤ 2 π

e o raio variando da origem até a curva limite vermelha

0 ≤ r ≤ a

Passo 4

Substituindo, então, na fórmula do momento de inércia não se esquecendo do Jacobiano

∬ D x 2 + y 2 ∙   a 2 a 2 + x 2 + y 2 d A =

∫ 0 2 π ∫ 0 a r 2 ∙ a 2 a 2 + r 2 ∙ J d r d θ =

∫ 0 2 π ∫ 0 a r 2 ∙ a 2 a 2 + r 2 r d r d θ

Pra resolver essa integral aí, vamos começar com a integral de dentro

∫ 0 2 π ∫ 0 a r 3 ∙ a 2 a 2 + r 2 d r d θ

onde vamos fazer uma substituição simples (não se esqueça que a é um número real)

a 2 + r 2 = t

d t = 2 r d r         →             r d r = d t 2

substituindo também os limites...

r = 0             →             a 2 + 0 2 = t           →             t = a 2

r = a 2             →             a 2 + a 2 = t           →             t = 2 a 2

na integral

∫ 0 2 π ∫ 0 a r 2 ∙ a 2 a 2 + r 2 r d r d θ = ∫ 0 2 π ∫ a 2 2 a 2 t - a 2   ∙ a 2 t d t 2   d θ

multiplicando tudo

∫ 0 2 π 1 2 ∫ a 2 2 a 2 a 2 - a 4 t   d t d θ =

∫ 0 2 π 1 2 a 2 t - a 4 ln ⁡ t a 2 2 a 2 d θ =

substituindo então os limites de integração

∫ 0 2 π 1 2 2 a 4 - a 4 ln ⁡ 2 a 2 - a 4 - a 4 ln ⁡ a 2 d θ =

dando uma simplificada nas coisas

∫ 0 2 π 1 2 a 4 + a 4 ln ⁡ a 2 2 a 2 d θ =

e lembrando que ln ⁡ 1 b = - ln ⁡ b

∫ 0 2 π 1 2 a 4 + a 4 ln ⁡ 1 2 d θ =

a 4 - a 4 ln ⁡ 2 2 2 π =

ganhamos então que

I p = π a 4 - a 4 ln ⁡ 2

Passo 5

Esse resultado, já é o momento de inércia! PORÉM... o problema nos pediu que ele estivesse em função da massa M . Bora coloca-lo então né?

A massa M pode ser encontrada facilmente fazendo

M = ∬ D ρ x ,   y d A

∬ D a 2 a 2 + x 2 + y 2 d A  

substituindo as polares

M = ∫ 0 2 π ∫ 0 a a 2 a 2 + r 2   J   d r d θ =

∫ 0 2 π ∫ 0 a a 2 a 2 + r 2   r   d r d θ

Integrando a de dentro...

∫ 0 2 π ∫ 0 a a 2 a 2 + r 2   r   d r d θ =

e lembrando que

a 2 + r 2 = t

d t = 2 r d r         →             r d r = d t 2

r = 0             →             a 2 + 0 2 = t           →             t = a 2

r = a 2             →             a 2 + a 2 = t           →             t = 2 a 2

e voltando para a integral onde vamos repetir a forma de resolução de integral

M = ∫ 0 2 π ∫ a 2 2 a 2 a 2 t   d t 2 d θ =

∫ 0 2 π 1 2 a 2 ln ⁡ t a 2 2 a 2 d θ =

∫ 0 2 π 1 2 a 2 ln ⁡ 2 a 2 a 2 d θ =

1 2 a 2 ln ⁡ 2 ∫ 0 2 π d θ =

M = π a 2 ln ⁡ 2

Passo 6

Agora é só encaixar essa massa aí na resposta do momento de inércia. Veja!

I p = π a 4 - a 4 ln ⁡ 2

I p = π a 4 - π a 4 ln ⁡ 2

como a 4 = a 2 a 2

I p = π a 4 - a 2 π a 2 ln ⁡ 2 =

concluímos que...

I p = π a 4 - a 2 M = π a 4 ln ⁡ 2 ln ⁡ 2 - a 2 M = π a 2 M ln ⁡ 2   - a 2 M = a 2 M 1 ln ⁡ 2 - 1 = a 2 M 1 - ln ⁡ 2 ln ⁡ 2

Resposta

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K