Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 1012345678911121314

Enunciado

  1. Uma lâmina homogênea tem a forma de um triângulo retângulo de catetos b e h . Ache o momento de inércia em função de sua massa M
  1. Em relação ao eixo x
  2. Em relação ao eixo y

Passo 1

LETRA A) Pow! A primeira coisa a se fazer aqui é sem dúvidas enxergar esse triângulo. Como ele é triângulo retângulo e possui lados (catetos) b e h , seu desenho é esse daqui

Colocando esse triângulo no plano cartesiano (para facilitar as contas, vamos coloca-lo com o ângulo reto no primeiro quadrante de forma que a base b esteja no eixo x):

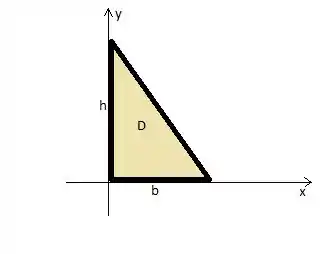
Passo 2

Momento de inércia em relação ao eixo x é...

I x = ∬ D y 2 ρ x ,   y   d A

Esse ρ x ,   y é a densidade da região, mas como essa região é homogênea, a função de densidade é uma constante k , logo podemos eliminá-la da integral:

I x = k ∬ D y 2   d A

Bem, para resolver essa integral dupla, vem comigo no processo para descrever a região D , o triângulo.

Passo 3

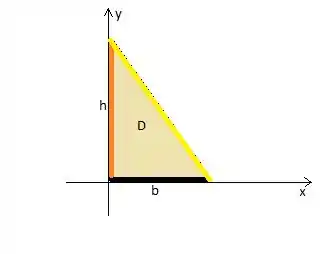
Pow, podemos descrever essa região como a do T i p o   2 (apenas por uma questão de preferência haha), onde y varia entre números reais, no caso de 0 até h

0 ≤ y ≤ h

enquanto que o x varia dessa reta vermelha até a amarela

R e t a   V e r m e l h a ≤ x ≤ R e t a   a m a r e l a

A reta Vermelha é easy para nós, a final de contas ela passa justamente pelo eixo y , ou... x = 0

0 ≤ x ≤ R e t a   a m a r e l a

Quanto à reta amarela... Bem...! Venha comigo ;)

Passo 4

Pow! Essa reta eu quero que você note que ela passa por x = b quando y é 0 e y = h quando x é 0 , logo, os dois pontos dessa reta é 0 ,   h   e   b ,   0 .

Para calculara equação dessa reta, preciso que recorde de como encontrar uma reta com dois pontos, afinal ela sai do ponto 0 ,   h , mas chega ao ponto b ,   0 . Então o ∆ y é

∆ y = 0 - h = - h

e ∆ x = b - 0 = b

colocando na forma geral de reta

y - y 0 = ∆ y ∆ x x - x 0

e substituindo ( x 0 ,   y 0 ) pela coordenada do pondo de chegada, ou seja

( x 0 ,   y 0 ) = b , 0

y - 0 = - h b x - b                 ⇒ a r r u m a n d o   d e   u m a   f o r m a   m a i s b e l a           y = - h b x + h

Como queremos 0 ≤ x ≤ R e t a   a m a r e l a

basta isolarmos o x em função do y , ali

          y = - h b x + h             →                 x = - b h y + b

logo...

0 ≤ x ≤ - b h y + b

Passo 5

Com esses dados em mãos, retornemos à integral dupla que queremos resolver...

I x = k ∬ D y 2   d A =

k ∫ 0 h ∫ 0 - b h y + b y 2 d x d y

Resolvendo essa integral como nos manda o figurino, ou seja, primeiro a de dentro

k ∫ 0 h ∫ 0 - b h y + b y 2 d x d y =

integral em x , y é constante e vaza

k ∫ 0 h y 2 ∫ 0 - b h y + b d x d y =

k ∫ 0 h y 2 x 0 - b h y + b d y =

substituindo os limites e dando aquela simplificada...

k ∫ 0 h y 2 - b h y + b d y =

k ∫ 0 h - b h y 3 + b y 2   d y =

integrando em y lembrando que b e h são números, obteremos...

k b y 3 3 - b h y 4 4 0 h =

k b h 3 3 - b h h 4 4 = k b h 3 3 - b h 3 4

I x = k b h 3 12

Passo 6

Mas aí é aquilo, neh! Encontramos o momento de inércia. Beleza! Um ponto! Mas o problema nos pede que deixemos em função da massa M .

Devemos encontrar a massa fazendo a integral dupla:

M = ∬ D ρ ( x ,   y )   d A

como a função de densidade é a constate k ...

M = ∬ D k   d A = k ∬ D d A =

k Á r e a   d e   D !

Que maravilha, neh?! Pois a área desse triangulo retângulo é easy:

Á r e a   d e   D = b a s e ∙ a l t u r a 2 = b ∙ h 2

= b h 2

Logo...

M = k b h 2

Substituindo no momento de Inércia

I x = k b h 3 12 =

k b h 2 ∙ h 2 6 =

M h 2 6

Passo 7

LETRA B) Pensa comigo: se virássemos toooodo o plano cartesiano (com o triângulo) de ladinho

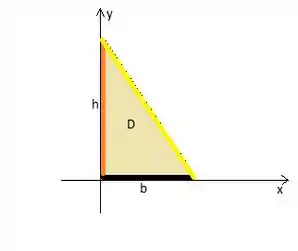
o momento de inércia em relação ao eixo y seria o mesmo momento de inércia do eixo x , calculado na letra a , porém trocando a letra h com a letra b . Isso pode acontecer, pois b e h são quaisquer, saca?

Então esquece esse verbo seria ali e coloca um será

I y = M b 2 6

Resposta

a )   M h 2 6

b ) M b 2 6

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K