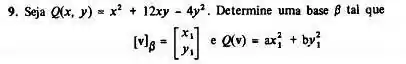
Passo 1
Agora temos que achar o sistema de coordenadas no qual a forma quadrática (dá no mesmo que se fosse formalmente uma quádrica) fica reduzida. Pra isso, como vimos na teoria, temos só que calcular os autovetores da matriz associada
Passo 2
Temos que:
Calculando os autovalores:
Logo os autovalores são e .
Logo o autovetor de norma associado é
Logo o autovetor de norma associado é
Como a base que procuramos é justamente aquela formada pelos autovetores: