Considere a quádrica dada por
Determine a equação reduzida(sem termos mistos, nem lineares quando possível) e identifique a quádrica.
Passo 1
Vamos identificar os coeficientes da nossa equação, se você não lembra, a equação geral das quádricas é dada por:
Para no nosso caso então, teremos:
TODOS OS OUTROS COEFICIENTES SERÃO IGUAIS A ZERO
Passo 2
Agora vamos colocar a nossa equação na forma matricial, pra quem não lembra, olha ela aí
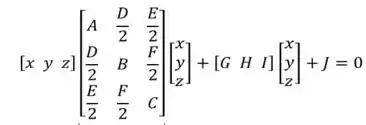

Calmaaaaa, é só a gente substituir os coeficientes que encontramos no passo 1.Substituindo tudo, ficamos com:
Belezinha, mas o que fazemos agora?
Passo 3
Vamos olhar agora para a matriz quadrada da nossa equação matricial, precisamos diagonalizar ela. Para isso encontramos os autovalores e os autovetores.
Agora, partiu calcular os Autovalores!
Temos
Se você não lembra a formulinha, é essa aqui ô:
Substituindo os valores,
Calculando esse determinante, achamos:
Logo,
Passo 4
Partiu calcular os Autovetores agora!
A formulinha é
Para , temos:
Com isso, dizemos que
Ou seja, o autoespaço de é gerado por , normalizando, teremos:
Para
é uma variável livre, então teremos que o autoespaço de é gerado por (1,0,0) e (0,-1, 1). Normalizando, obtemos:
Com isso, conseguimos montar nossa matriz dos autovalores e dos autovetores e substituir em uma nova fórmula matricial:
Sendo e
CUIDADO: A ordem dos autovalores e autovetores importa, então cuidado para não trocar eles!!
Passo 5
Substituindo, teremos
Resolvendo essa coisa “amigável” aí, temos:
Completando quadrados,
Atribuindo:
Ficamos com:
Mudando o sinal e dividindo por 2, temos:
A quádrica é uma hiperboloide de uma folha.
Pode comemorar, ACABOOOOOU!!!

Resposta
A quádrica é um hiperboloide de uma folha