Considere a quádrica de equação
a) Identifique e esboce .
b) Para cada um dos planos a seguir, identifique . Caso seja uma cônica não degenerada, indique as coordenadas de um foco e de um vértice de .
i)
ii)
iii)
Passo 1
a) Nossa equação é assim:
Completando os quadrados em , teremos:
Dividindo tudo por -2:
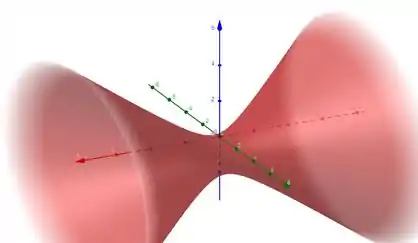
Isso nos dá um hiperboloide de uma folha trasladado no eixo . Ele está ao longo do eixo , que está negativo.
Passo 2
b) i) Substituindo na equação para encontrarmos a intersecção, vamos ter
Analisando essa equação, vemos que ela é uma elipse com o eixo maior ao longo da reta e seus parâmetros são , e .
Seus focos são e .
Seus vértices são
ii) Substituindo vamos ter
Isso nos dá uma hipérbole com eixo ao longo do eixo e parâmetros , e .
Portanto, seus focos são e .
Seus vértices são e .
iii) Substituindo , temos
Isso nos dá uma hipérbole degenerada, um par de retas concorrentes.
Resposta
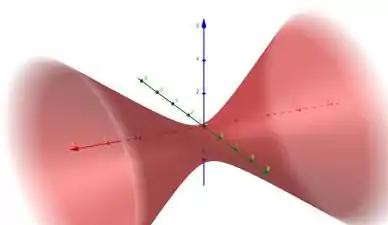
a) Hiperboloide de uma folha
b) i)
e .
ii)
e .
e .
iii) ; hipérbole degenerada.