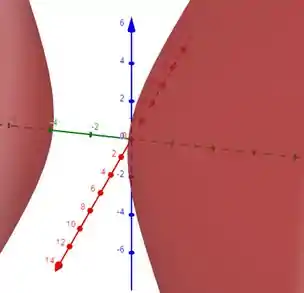
O conjunto dos pontos do espaço, cuja distância até o ponto é igual ao dobro de sua distância até o plano , é uma quádrica.
Ache a equação desta quádrica, identifique (ache centro e, semieixos ) e esboce.
Passo 1
Show de bolinhas meus amores, dado o ponto e o plano queremos encontrar o conjunto dos pontos cuja distância até o ponto , , seja igual ao dobro da distância do ponto até o plano :
Iradoso, então se a gente abrir essas distâncias temos que:
E para a distancia de um ponto ao plano, podemos usar a fórmula:
Dado , temos que:
E nossa igualdade entre as distâncias na verdade pode ser reescrita como:
Passo 2
Belezoca, e agora pra reorganizar esses termos, podemos elevar os dois lados ao quadrado:
Logo:
Abrindo os produtos notáveis, obtemos:
E se a gente for malandrão e completar o quadrado para , descobrimos que:
Logo nosso quádrica pode ser reescrita como:
Reorganizando novamente:
E dividindo tudo por , chegamos na quádrica:
Passo 3
E pela equação
Vemos que se trata de um hiperbolóide de duas folhas, cujo eixo distinguido é (devido o sinal invertido). Enquanto os semieixos são:
E como o eixo distinguido está em , temos que o vértice do hiperbolóide também vai estar. Então substituindo o ponto na equação, vamos obter:
Portanto e de modo que os vértices são:
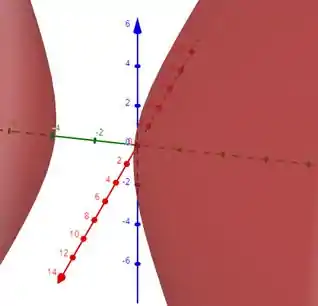
Resposta