Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 22 – seção Problema adicionais 66.
(Cap 22 Ex - 66) Um próton e um elétron ocupam dois vértices de um triângulo equilátero de lado m. Qual é o módulo do campo elétrico no terceiro vértice do triângulo?
Passo 1
Falaii pessoal, tudo belezinha?
Bora para mais uma?
Bem, a ideia desse problema é descobrir o campo elétrico no vértice de um triangulo equilátero de lado , onde os outros dois vértices são formados por um próton e um elétron.
Sabemos que a carga do próton é positiva e a do elétron é negativa. Sendo assim, os vetores do campo elétrico têm direções contrárias. É mais fácil entender desenhando:
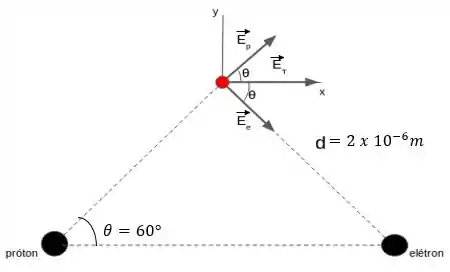
Como, podemos observar na figura, o campo elétrico de um elétron (carga negativa)
sempre vai em direção a ele, e o campo do próton (carga positiva) sempre está saindo dele. Dessa forma, o campo resultando aparece ali no meio deles, na figura.
Você pode estar se perguntando porquê os dois ângulos são iguais ali na figura: bom, o próton e o elétron possuem a mesma carga, em módulo, e estão distantes iguais do ponto que queremos estudar. Logo, também em módulo, vão possuir o mesmo campo elétrico. Com isso, o vetor resultante ficará bem no meio das componentes mesmo!! Pois elas são iguais em módulo!
Além disso, por trigonometria, vemos que . (A explicação se dá por ângulos alternos).
Agora, podemos calcular somente o valor do campo elétrico, sabendo que vai ser, justamente, a soma das componentes horizontais de e .
Passo 2
O problema nos pede apenas o módulo do campo elétrico. Relembrando a formula do módulo do campo elétrico:
Como a carga do elétron e do próton são iguais:
Por relação de triângulos , como queremos calcular o eixo , que é o cateto adjacente:
Substituindo os valores:
Lembre-se de verificar se a calculadora está em graus.
Show! Fechamos mais uma!