Considere uma corda cuja tensão e a densidade linear são dadas por e , respectivamente, e a equação de movimento é representada por

1. Considerando uma onda nesta corda escrita por

Obtenha em termos de e .

2. Qual é o período da onda (2)? Tem que justificar a definição do período utilizado.
3. Considere uma extremidade fixa em . Depois que a onda (2) atinge a extremidade a forma da onda refletida pode ser escrita

Calcule o valor de B.

Agora vamos usar a equação de onda pra resolver o resto da parada:

Então:

Agora, olhando pra cá:

A gente pode manipular isso e chegar em:

Show? Mas lembrado que:

b):

Como o comprimento de onda é dado como conhecido, afinal de contas ele aparece na fórmula, temos que:

Então:

c):

Pra a gente entender isso melhor, a gente pode analisar apenas um pulso dessa corda, ao invés de toda a onda. Um pulso, quando atingir uma extremidade fixa, vai mudar de direção e vai ficar inclinado para baixo, assim:

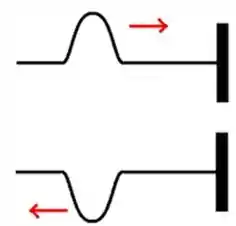
Legal, e o que acontece se essa pulso se encontrar com outro ali na fronteira, ou seja, na extremidade?

O que acontecerá se ele se encontrar com o pulso incidente?

Como um estará para cima e o outro pra baixo, eles vão se anular, certo?

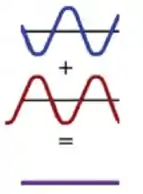
Mais ou menos como acima. Bem, é isso, na ponta existira um nó, como em toda onda estacionária, afinal, essa onda refletida na extremidade vai voltar e gerar uma onda estacionária.

Então, o que podemos dizer sobre isso matematicamente. A função da onda incidente é:

Vamos chamar de:

E a da refletida:

Vamos chamar de:

Então, podemos dizer que a soma das duas funções em dá zero:

Só que, qual condição garante isso ai acima? Bom, vamos pensar: Se ambos os ângulos forem múltiplos de , então a igualdade acima pode ser escrita. Mas se ambas as fases forem múltiplas de , podemos escrever:

Ou seja, a diferença entre as fases é um múltiplo impar de Exemplo:

Etc.

Então:

Como