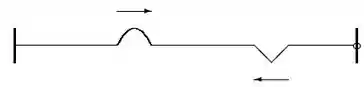
Dois pulsos de formas diferentes se propagam com velocidade numa corda esticada de comprimento . A corda tem sua extremidade esquerda fixa num suporte, mas a extremidade direita pode oscilar livremente. Num dado instante a situação da corda é aquela mostrada na figura. Esta EXATA situação irá se repetir exatamente após um intervalo de tempo mínimo dado por:
Passo 1
Galera, nesse tipo de exercício é legal a gente fazer um esquema para identificarmos mais facilmente os diferentes instantes em que se encontra a propagação da onda na corda.
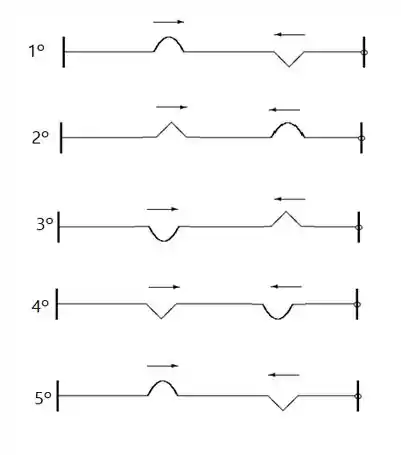
Cada trajeto da propagação da onda representa um comprimento da corda esticada. Logo:
Então temos um trajeto total percorrido de , até que a situação descrita no enunciado se repita. Temos então que:
Resposta
Letra d
Exercícios de Livros Relacionados
A Figura 15-30 mostra um pulso no tempo t = 0 movendo-se para a direta. (a) Neste instante, quais são os segmentos da corda que estão se movendo para cima? (b) Quais são os segmetos que estão se moven
No tempo t = 0, a forma de um pulso de onda em uma corda é dada pela função y x , 0 = 0.120 m 3 / ( 2.00 m 2 + x 2 ) , onde x está em metros. (a) Esboce y( x ,0 ) versus x. (b) Dê a função de onda y(
Duas ondas, y 1 = 2,50 m m s e n [ 25,1 r a d m x - ( 440 r a d / s ) t ] y 2 = 1 , 50 m m s e n [ 25,1 r a d m x + ( 440 r a d / s ) t ] Propagam-se em uma corda esticada. (a) Plote a onda resultante
A mesma corda descrita no Problema 1 está com uma extremidade amarrada num poste. A outra, inicialmente em repouso na posição de equilíbrio, é deslocada de 10c m para cima, com velocidade uniforme, en
Duas cordas muito longas, bem esticadas, de densidades lineares diferentes μ 1 e μ 2 , estão ligadas uma à outra. Toma-se a posição de equilíbrio como eixo dos x e a origem O no ponto de junção, sendo