Uma corda de material homogêneo, de 20 m de comprimento e massa de 2 kg está esticada sob uma tensão de 10 N.
(b) Com a corda novamente em repouso, sujeita à mesma tensão e na posição de equilíbrio, amarra-se a extremidade direita a um poste enquanto a esquerda é deslocada 10 cm para cima, com velocidade uniforme entre t = 0 s e t = 0,5 s. Em t = 0,5 s, a mesma extremidade é deslocada para baixo com magnitude da velocidade reduzida à metade até o instante t = 1,5 s e depois mantida fixa na posição de equilíbrio. Faça 2 desenhos, um para a forma da corda no instante t = 1,7 s, outro no instante t = 3,7 s. NÃO é necessário deduzir a solução da equação de onda neste caso.
Passo 1
(b) Esse enunciado é um pouco confuso, mas vamos entender por partes!
Como a corda está sujeita à mesma tensão, então a velocidade de propagação da onda continua igual:
A extremidade esquerda é deslocada para cima, com velocidade constante, da altura zero () até a altura de 10 cm (). Então a corda vai subindo linearmente até a altura de 10 cm.
Quando a corda estiver no máximo (), a parte mais baixa do pulso já vai ter se propagado em uma distância
Ou seja, no instante , temos o máximo da onda (10 cm) na extremidade esquerda e a parte mais baixa na posição :

Passo 2
Depois de , “a mesma extremidade é deslocada para baixo com magnitude da velocidade reduzida à metade até o instante t = 1,5 s”.
Então ela vai sendo puxada pra baixo, mais lentamente do que foi pra cima, por , até a posição de equilíbrio, .
No gráfico, vamos ver, logo depois da subida, uma descida mais lenta. Em , a parte mais baixa da descida () vai estar na extremidade esquerda.
Já em , a parte mais baixa da descida vai estar em
Já a parte mais alta da onda, o vale, vai estar em
Juntando as informações,
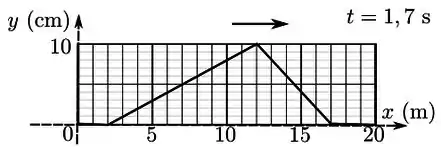
Passo 3
Agora falta desenhar o gráfico para .
O início do pulso atinge a extremidade direita da corda em
O final do pulso atinge depois ou seja, .
Ao atingir uma extremidade fixa, a onda volta, mas com a amplitude invertida.
Se em 3,5 s o final do pulso fecha até a extremidade direita, em , o final do pulso terá voltado
O gráfico vai ficar, então,
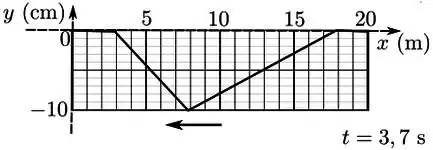
Resposta
Ei, a resposta está no passo a passo :)