Considere uma onda dada por que atinge a extremidade de uma corda, fixa em Neste caso, qual é a forma da onda refletida?
Passo 1
Bom, galera, aqui a gente vai ter que usar o conceito de solução geral da equação de onda unidimensional:
A solução geral é:
O que vamos fazer aqui? Bem, o enunciado nos deu uma função parecida com a primeira equação acima. A nossa missão é achar a outra:
No entanto, vamos prestar atenção numa coisa. Antes que a onda bata lá em , nós consideramos que:
Vamos lá.
Passo 2
Bom, a onda inverte a sua fase em .:
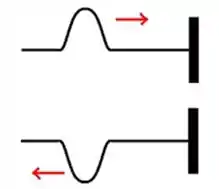
Então, ali .
Show? Então vamos escrever:
Passo 3
Beleza?
Bom, mas o produto de uma velocidade com tempo nos dá uma distância, certo? Então podemos fazer isso:
Então:
Ok. Mas as equações acima são funções. Então podemos usar mudança de variáveis ali.
Como queremos encontrar o valor de:
Podemos chamar:
Assim:
Pronto (:
d)
Resposta
d)