Uma corda homogênea, de massa e comprimento , está presa em ambos os extremos e submetida a uma tensão . A corda vibra num dado modo normal. Observa-se que um certo ponto da corda leva para ir de seu deslocamento máximo positivo ao mínimo e voltar ao máximo.
Quantos ventres de oscilação estão presentes na corda?
- 3
- 1
- 2
- 4
- 6
Passo 1
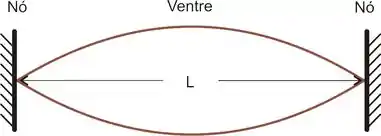
Quando falamos de ventre de oscilação em uma corda, queremos saber as regiões onde a oscilação é máxima, essa região é chamada de Ventre; e a letra indica os pontos onde a oscilação é mínima, denominada de Nó.
Para começar vamos definir algumas funções do comprimento e da velocidade da onda que serão úteis para resolver nosso exercício:
, e ,
onde é a densidade de massa linear.
Passo 2
Precisamos achar uma equação na qual a gente consiga encontrar o termo . Da teoria de oscilação em uma corda, vimos que:
Sendo um termo definido em função de , vamos agora deixar a equação com uma cara de modo que nossa variável seja a variável independente:
Logo, substituindo os termos na equação descrita acima:
Resposta
Letra D