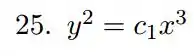
Passo 1
Primeiro vamos lembrar um pouco das equações que precisamos quando tratamos de trajetória ortogonal. Vamos achar a EDO associada à nossa equação no formato.
E depois acharemos a EDO da trajetória ortogonal da seguinte forma.
Vamos fazer isso com a nossa equação.
Sendo assim, a EDO que devemos resolver será.
Passo 2
Antes de resolvermos a EDO devemos trocar por uma função de .
Logo a EDO será.
Agora basta resolver.
Passo 3
Colocando no formato de equação separável.
Integrando as duas equações.
Chamando
Resposta
Exercícios de Livros Relacionados
y = k x Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
y 2 = k x 3 Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.6 - k x 2 + y 2 = 1
Os dados na Tabela 9.4 foram coletados com um detector de movimento e um CBLTM ( computer based learning - aprendizagem assistida por computador) por Valerie Sharritts, uma professora de matemática da
12 - Encontre a família de soluções de determinada equação diferencial e a família de trajetórias ortogonais. Esboce as duas famílias. xd x+yd y=0 xd y-2 yd x=0