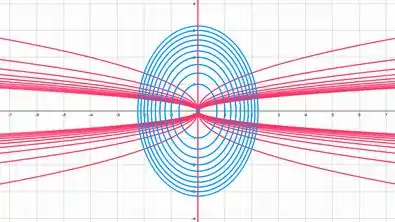
Determine as trajetórias ortogonais da família de curvas , onde é uma constante arbitrária. Faça uma figura ilustrando as famílias.
Passo 1
Lembra lá o que são trajetórias ortogonais: são nada mais que uma família de curvas que corta outra família de curvas de maneira ortogonal, ou seja, fazendo .
A primeira coisa a ser feita é determinar a EDO da própria família, isto é, determinar seus coeficientes angulares. Fazemos isso derivando com respeito a a equação que define a família. Ficando com:
Como
Segue o bonde!
Passo 2
Agora precisamos encontrar a família que tenha um coeficiente angular (vou denotar por de novo) que respeite a seguinte relação, já que precisamos que sejam ortogonais:
Resolvendo a EDO
OPAAA! Essa família é de elipses!
Passo 3
Desenhando as famílias:
Resposta
Exercícios de Livros Relacionados
y = k x Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
y 2 = k x 3 Encontre as trajetórias ortogonais da família de curvas usando uma calculadora (ou um computador). Desenhe vários membros de cada família na mesma tela.
Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.6 - k x 2 + y 2 = 1
Os dados na Tabela 9.4 foram coletados com um detector de movimento e um CBLTM ( computer based learning - aprendizagem assistida por computador) por Valerie Sharritts, uma professora de matemática da
12 - Encontre a família de soluções de determinada equação diferencial e a família de trajetórias ortogonais. Esboce as duas famílias. xd x+yd y=0 xd y-2 yd x=0