Resolva o seguinte problema de valor inicial por Transformada de Laplace. Indique sempre a propriedade da tabela de transformadas de Lalace sendo utilizada em cada passo.
Passo 1
Fala povo, tudo certinho? Vamos lá? Pra começar, quando usamos transformadas, podemos fazer a transformada nos dois lados da equação:
E das propriedades das transformadas, podemos ainda fazer:
Opa, transformadas! Vamos ver uma de cada vez, ok? Na ordem de leitura, usamos a propriedade pra fazer a primeira transformada:
![]()
Sendo assim, temos:
Do enunciado, tiramos os valores da função para e da sua derivada no mesmo instante:
Show, agora pra segunda transformada a ideia vai ser a mesma, usaremos também a regra :
E pra terceira transformada, temos:
Então o lado esquerdo da equação ganha essa cara simpática aqui ó:
Agora, pra transformada que ficou faltando, do lado direito, por mais feia que ela seja, dá sim pra resolver. Só que não vai dar pra usarmos nenhuma das propriedades que a prova dá, então vamos usar a definição de transformadas:
E pra resolver esse cara feio, precisamos ainda de uma definição importantíssima do Delta de Dirac, que é sua relação com a função degrau:
Te prometo que, usando isso, essa função sai! Vamos chamar aí de:
De forma que temos a integral:
Pra resolver. Po, produto de funções né? Isso daí se resolve usando integração por partes! Saca só:
A integral fica:
Note que, se
Temos
De forma que, temos:
E também temos esse carinha aqui ó:
Sendo assim, o resultado da integral vira, finalmente:
Ou seja:
Ufa, fizemos já todas as transformadas! Juntando tudo, temos:
Podemos ainda aproveitar que esse denominador em comum é um trinômio quadrado perfeito pra simplificar ainda mais, saca só:
Vamos ter:
E nos próximos passos a gente vai se preocupar em inverter pra achar ! Vamo que vamo!
Passo 2
Pra começar, a mesma propriedade que vimos pra transformada, vale pra transformada inversa! Ou seja galera, vamos ficar com essa fórmula linda aqui:
Temos então três transformadas inversas pra achar! Pra primeira, podemos usar essas propriedades abaixo:
![]()
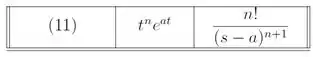
De forma que:
Onde:
E é ai que entra a propriedade , pois se compararmos os denominadores e , vemos que:
Assim, temos:
A primeira transformada inversa ta fechada então:
Loooooogo:
Passo 3
Ok eu sei, o passo anterior foi beeeeem doido, mas calma que sobrou uma transformada inversa ainda
Por sorte, esse carinha não vão dar tanta dor de cabeça pra gente, uma vez qu temos as propriedade abaixo pra ajudar:
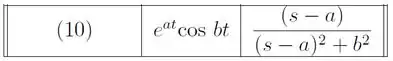
Ok mas não é tããão parecido assim o nosso caso? Bem, se não é, bora fazer ser! Saca só:
Onde a primeira transformada é exatamente o caso pra e . Claro que podíamos ainda cortar um em cima e outro em baixo e cair exatamente na regra:
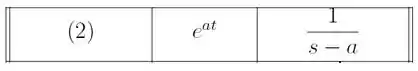
Dá no mesmo, viu? O importante é saber que:
Agora pra transformada inversa que sobrou, na verdade, nem precisamos nos preocupar muito! Afinal, resolvemos exatamente ela no passo anterior! E tínhamos achado esse rapaz simpático aqui:
Então feshow, temos:
Passo 4
Quase lááááá galera, falta só juntar os resultados. No início do passo 2, vimos que:
No fim dele, vimos que:
E no fim do passo 3, vimos que:
Falta o que? Nadaaa galera! Só juntar! A resposta final será: