Resolva por Transformada de Laplace o seguinte problema de valor inicial, justificando todas as propriedades da tabela de Transformada de Laplace usadas.
Onde e
Passo 1
Fala povo, tudo certinho? Vamos lá? Pra começar, quando usamos transformadas, podemos fazer a transformada nos dois lados da equação:
E das propriedades das transformadas, podemos ainda fazer:
Opa, transformadas! Vamos ver uma de cada vez, ok? Na ordem de leitura, usamos a propriedade pra fazer a primeira transformada:
![]()
Sendo assim, temos:
Do enunciado, tiramos os valores da função para e da sua derivada no mesmo instante:
E pra segunda transformada, temos:
Então o lado esquerdo da equação ganha essa cara simpática aqui ó:
Agora, pra transformada que ficou faltando, do lado direito, por mais feia que ela seja, dá sim pra resolver. Basta a gente olhar com calma as propriedades das transformadas e ver que ela encaixa direitinho na integral de convolução:

De forma que:
É o mesmo que dizer:
E a transformada desses cara será:
Logo, usando as propriedades abaixo, achamos:
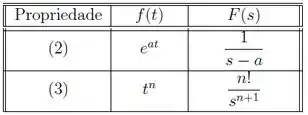
Ficamos então com:
Passo 2
Tá galera, não acabamos, mas calma que não falta muito. O ultimo resultado é meio feio e não ajuda a gente. Não dá pra usar nenhuma propriedade de transformadas. Mas bem, se a gente usar frações parciais, talvez ajude em algo. Portanto, separando isso dessa forma:
Vemos que cada termo dessa forma tem uma cara mais amigável que, quando fizermos a transformada inversa, vai sair direitinho! Falta definir quem são essas constantes. Pra isso, bora colocar todo mundo no mesmo denominador:
Removendo o denominador nos dois lados e aplicando a distributiva, temos:
Colocando os termos em comum em evidência, temos:
O que gera um sistema grande, eu sei, mas vamos que vamos, olha só:
Por sorte, a última linha já ajuda a gente a beça, pois achamos:
Jogando esse valor na quarta equação, temos:
Com o valor de , reduzimos o problema para:
Somando a primeira e a segunda equação, achamos:
E somand essas duas, achamos:
Com o valor de , achamos :
E logo:
Mas como:
Temos, finalmente:
E agora que sabemos tudo, fechamos a modelagem de
Passo 3
Ok eu sei, o passo anterior foi beeeeem doido, mas calma que sobrou só pegar a transformada inversa daquele monstrão.
Usando as propriedades das transformadas inversas:
Pra última transformada, podemos ainda separá-la, de forma a obter:
O que nos deixa com:
Opa, olha que bacana, todas as 5 transformadas inversas saem diretamente das nossas propriedades. As que usaremos serão:
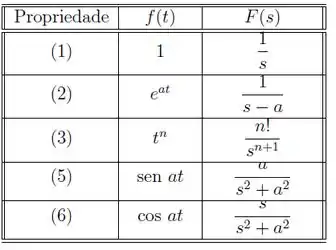
Ufa! Cabamos!