Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Laplace em circuitos

Ver Teoria
Exercício 31245678910111213

Enunciado

Calcule o valor de v o ( t ) no circuito:

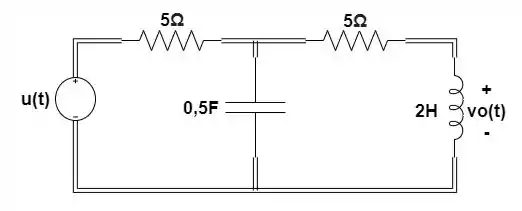
Passo 1

Primeiro passo é substituir os elementos por suas transformadas de Laplace:

u t ⟶   1 s

5 Ω ⟶   5

1 2 F ⟶   1 s C =   1 s 1 2 =   2 s

2 H ⟶ s L = 2 s

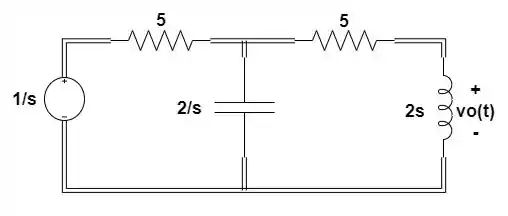
Passo 2

Agora vamos estipular as correntes em cada uma das malhas:

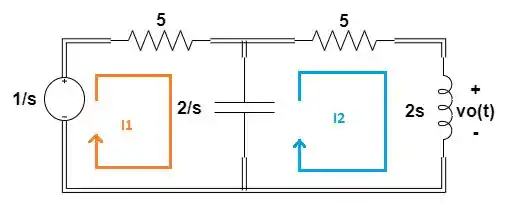
Passo 3

Vamos analisar cada uma das malhas normalmente com a LKT. Analisando a malha 1, temos:

1 s - 5 I 1 -   2 s   I 1 -   I 2 = 0

Analisando a malha 2:

-   2 s   I 2 -   I 1 - 5 I 2 - 2 s I 2 = 0

Passo 4

Colocamos a partir da segunda equação, a corrente I 1 em função da corrente I 2 :

-   2 s   I 2 -   I 1 - 5 I 2 - 2 s I 2 = 0

-   2 s I 2 + 2 s I 1 - 5 I 2 - 2 s I 2 = 0  

2 s I 1 =   2 s I 2 + 5 I 2 + 2 s I 2

I 1 = I 2 s 2 +   5 s 2 + 1

Passo 5

Substituindo na primeira equação:

1 s - 5 I 1 -   2 s   I 1 -   I 2 = 0

1 s - 5 I 2 s 2 +   5 s 2 + 1 -   2 s I 2 s 2 +   5 s 2 + 1 +   2 s I 2   = 0

1 s -   I 2 s 2 +   5 s 2 + 1   2 s + 5 + 2 s I 2 = 0

1 s -   I 2 5 + 25 s 2 + 5 s 2 +   2 s + 5 + 2 s +   2 s   I 2 = 0

1 s =   I 2 10 + 2 9 s 2 + 5 s 2

1 s =   I 2 10 s 2 + 29 s + 20 2

I 2 = 2 s ( 10 s 2 + 29 s + 20 )  

Passo 6

Sabemos que:

v 0 s =   2 s I 2

v 0 s =   2 s 2 s ( 10 s 2 + 29 s + 20 )  

v 0 s =   4 ( 10 s 2 + 29 s + 20 )  

v 0 s =   4 s + 1,13 ( s + 1,77 )

Passo 7

Aplicando a inversa de Laplace:

L - 1 1 s - a s - b =   1 a - b ( e a t - e b t ) ,   a ≠ b

L - 1 4 s - ( - 1,13 ) s - ( - 1,77 ) =   4 [ - 1,13 - ( - 1,77 ) ] ( e - 1,13 t - e - 1,77 t )

v 0 t = 4 1,77 - 1,13 ( e - 1,13 t - e - 1,77 t )

v 0 t = 6,25 ( e - 1,13 t - e - 1,77 t ) V

Resposta

v 0 t = 6,25 ( e - 1,13 t - e - 1,77 t ) V

Exercícios de Livros Relacionados

Um sistema com única entrada e única saída é descrito pelo modelo de estados a seguir: x 1 = 2 x 1 - x 2 + 3 z x 2 = - 4 x 2 - z y = 3 x 1 - 2 x 2 + z Qual das matrizes seguintes é incorreta?a) A = 2
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .
Seja v s = 20 cos ⁡ a t V no circuito da Figura. Determine ω 0 , Q e B , visto pelo capacitor.
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar