Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Laplace em circuitos

Ver Teoria
Exercício 13123456789101112

Enunciado

Dado o circuito a seguir, determine a resposta natural da descarga do capacitor no circuito a seguir utilizando a transformada de Laplace.

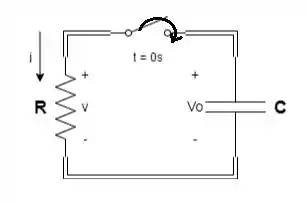
Passo 1

Primeiro vamos escrever as equações referentes ao resistor:

v t = R * i t

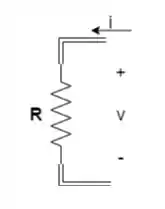
Aplicando a transformada de Laplace:

V s = R * I ( s )

Então mantemos o mesmo circuito no domínio de s:

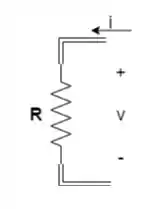
Passo 2

Agora vamos fazer o mesmo com o capacitor:

i t = C * d v d t

d v d t =   i ( t ) C

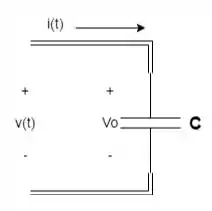
Aplicando a transformada de Laplace:

L d v d t = s V s - v ( 0 - )

L i ( t ) C = I ( s ) C

Logo, aplicando Laplace em d v d t =   i ( t ) C , temos:

s V s - v 0 - =   I ( s ) C

s V s =   I ( s ) C +   v 0 -

V s =   I ( s ) s C + v 0 - s  

Passo 3

Podemos substituir o circuito no domínio do tempo por um circuito no domínio de s da sequinte maneiraque corresponde a equação que encontramos:

V s =   I ( s ) s C + v 0 - s  

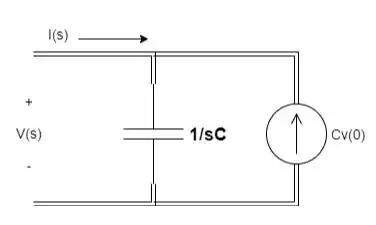
Passo 4

Agora podemos acoplar os dois circuitos e analisar a tensão de descarga no capacitor:

I s =   I 1 s +   I 2 s

C v 0 =   V c   ( s ) R +   V c   ( s ) 1 R C

C v 0 =   V c   s 1 R + 1 1 R C

V c   s = C v 0 s C +   1 R

V c   s = v 0 C +   1 R C

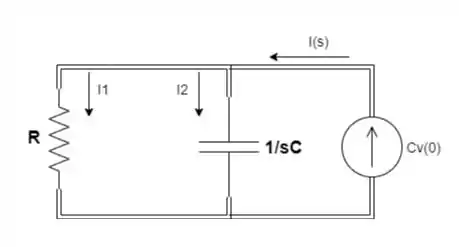
Passo 5

Vamos fazer a transformada inversa de Laplace:

L - 1 [ V c   s ] = L - 1 [ v 0 C +   1 R C ]

v c t =   V 0   e - t R C

Pronto, pessoal, encontramos a mesma equação que já conhecíamos da descarga do capacitor com um resistor, mas agora através de Laplace.

Passo 6

Resposta

v c t =   V 0   e - t R C

Exercícios de Livros Relacionados

Um sistema com única entrada e única saída é descrito pelo modelo de estados a seguir: x 1 = 2 x 1 - x 2 + 3 z x 2 = - 4 x 2 - z y = 3 x 1 - 2 x 2 + z Qual das matrizes seguintes é incorreta?a) A = 2
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .
Seja v s = 20 cos ⁡ a t V no circuito da Figura. Determine ω 0 , Q e B , visto pelo capacitor.
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar