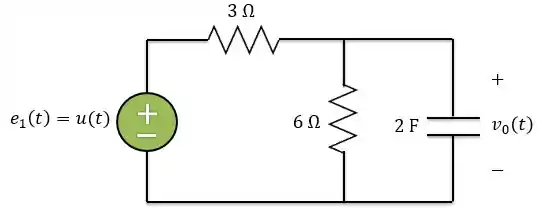
Escreva uma equação nodal descrevendo o circuito abaixo para . Se a capacitância estava descarregada para , determine Determine a transformada inversa de pelo método das frações parciais.
Passo 1
Antes de mais nada, vamos determinar a condição inicial de .
Em , a fonte de tensão vale zero, já que para . Ou seja, podemos considerá-la desligada. Além disso, o enunciado disse que o capacitor estava descarregado. Logo, não há circulação de corrente no circuito e
Como a tensão no capacitor não pode variar instantaneamente, assim como a corrente no indutor, temos que
Passo 2
Agora, vamos encontrar a EDO que descreve no circuito para Para , a fonte de tensão passa a funcionar e vale , já que para o degrau unitário vale um, Então, a gente tem esse circuito aí.
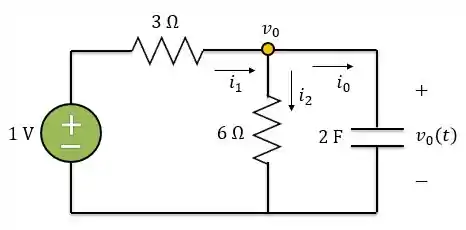
Aplicando LCK ao nó do circuito,
Logo,
Arrumando os termos,
Simplificando,
Que podemos escrever também desta maneira:
Passo 3
Agora que encontramos a EDO não homogênea, precisamos resolvê-la utilizando Transformada de Laplace. Para isso, primeiro precisamos encontrar uma expressão para .
Para relembrar como funciona, vamos aplicar transformada de Laplace em cada termo da EDO:
Quando temos uma constante sempre consideramos ela multiplicada pelo degrau unitário, porque para .
Logo,
Como,
Portanto, a nossa equação transformada é
Substituindo a condição inicial que encontramos
Temos,
Simplificando,
Isolando a transformada da tensão,
Passo 4
Agora que encontramos a expressão para , vamos utilizar o método de expansão em frações parciais.
Expandindo em frações parciais,
Agora, precisamos determinar as constantes e .
Como a raiz de é zero, para temos
Simplificando,
Vamos seguir o mesmo processo para encontrarmos .
Como a raiz de é , temos:
Simplificando,
Substituindo o valor de cada constante, temos que
Passo 5
Agora que encontramos a expressão para em frações parciais, vamos aplicar a Transformada inversa de Laplace:
Como,
Portanto,
A gente também pode escrever a resposta acima da seguinte maneira: