Determine as respostas ao degrau unitário e ao impulso no circuito abaixo.
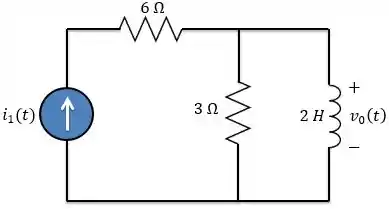
Passo 1
O enunciado nos pede a tensão no indutor quando a corrente da fonte for primeiro um degrau unitário e depois um impulso unitário . Vamos começar!
Passo 2
Primeiro, vamos analisar o caso em que Como a fonte de corrente é um degrau unitário, até o instante , não há circulação de corrente no circuito e para a fonte de corrente vale . Logo, para vamos analisar o circuito abaixo.
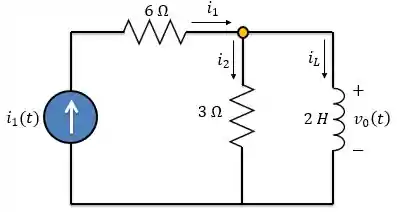
Sabemos que a tensão no indutor tem a seguinte relação:
E como o indutor está em paralelo com o resistor de , eles possuem a mesma tensão.
Aplicando LCK no nó:
Como, para , .
Logo,
Passo 3
Aplicando Transformada de Laplace na expressão acima, temos
Como a fonte de corrente é um degrau unitário, até o instante , não há circulação de corrente no circuito. Logo, para . Lembrando que a corrente no indutor não pode variar instantaneamente, então:
Portanto, substituindo a nossa condição inicial, temos:
Isolando a transformada da corrente,
Passo 4
Agora que encontramos a expressão para , vamos utilizar o método de expansão em frações parciais.
Expandindo em frações parciais,
Agora, precisamos determinar as constantes e .
Para temos
Simplificando,
Vamos seguir o mesmo processo para encontrarmos .
Simplificando,
Substituindo o valor de cada constante, temos que
Passo 5
Agora que encontramos a expressão para em frações parciais, vamos aplicar a Transformada inversa de Laplace:
Portanto,
Passo 6
Agora que encontramos a corrente que passa pelo indutor, finalmente podemos encontrar o valor de Sabemos que:
Substituindo,
Logo,
Passo 7
Agora, precisamos encontrar para quando . No instante , um impulso de corrente no indutor causaria uma corrente infinita passando por ele, o que não é possível. Logo, o impulso de corrente fornecido pela fonte deve passar somente pelos resistores.
Quando esse impulso unitário de corrente passa pelo resistor de , ele gera um impulso de tensão no resistor e, consequentemente, no indutor, já que eles estão em paralelo. Portanto podemos dizer que:
Passo 8
Encontramos o valor de no instante . Agora temos que calcular para .
Quando , a EDO que a gente tinha encontrado fica assim:
Aplicando Transformada de Laplace na expressão acima, temos
Como,
Temos:
Isolando a transformada da corrente,
Passo 9
Agora que encontramos a expressão para em frações parciais, vamos aplicar a Transformada inversa de Laplace:
Portanto,
Passo 10
Agora que encontramos a corrente que passa pelo indutor para , finalmente podemos encontrar o valor de Sabemos que:
Substituindo,
Logo, a expressão geral para quando a fonte de corrente é um degrau unitário é: