Considere o circuito da figura. Determine o valor da tensão no capacitor supondo que o valor de e que em flui uma corrente igual a através do indutor, e no capacitor tem uma tensão de .
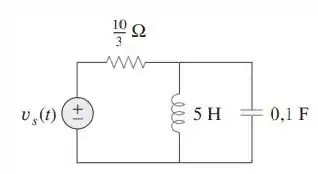
Passo 1
Primeiro vamos desenhar o circuito em domínio Laplace. Incorporamos a condição inicial e então adicionamos uma fonte de corrente paralela ao indutor (por causa da corrente de que flui no indutor).
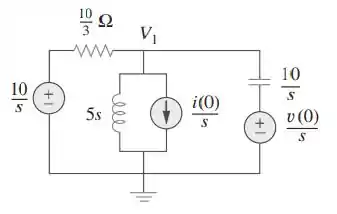
Passo 2
Agora podemos fazer análise nodal simples no nó de cima (o nó cuja tensão é )
Onde e
Agora, vamos simplificar a expressão para chegar no jeito mais fácil de fazer a Transformada de Laplace inversa:
Agora fica fácil aplicar a transformada de Laplace Inversa:
Resposta
Exercícios de Livros Relacionados
Um sistema com única entrada e única saída é descrito pelo modelo de estados a seguir: x 1 = 2 x 1 - x 2 + 3 z x 2 = - 4 x 2 - z y = 3 x 1 - 2 x 2 + z Qual das matrizes seguintes é incorreta?a) A = 2
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .
Seja v s = 20 cos a t V no circuito da Figura. Determine ω 0 , Q e B , visto pelo capacitor.
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar