Determine no circuito da figura supondo condições iniciais zero.
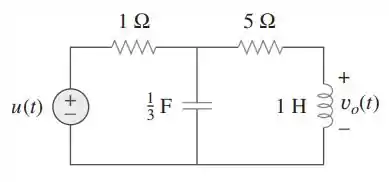
Passo 1
Primeiro, vamos passar cada elemento para o domínio de Laplace, ou seja, domínio s:
(como )
Passo 2
Agora, vamos desenhar o novo circuito no domínio de Laplace.
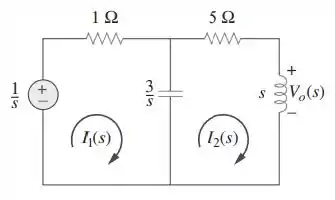
Passo 3
A partir daí, podemos fazer análise de malhas de uma forma simplificada
Na malha 1:
Na malha 2:
Agora, substituindo a equação de na equação da malha 1:
Simplificando (multiplicamos tudo por :
E então:
Passo 4
Achamos a tensão no domínio de Laplace, mas agora precisamos fazer a transformada inversa a partir das tabelas de transformada inversa para chegarmos na resposta em função do tempo:
Resposta
Exercícios de Livros Relacionados
Um sistema com única entrada e única saída é descrito pelo modelo de estados a seguir: x 1 = 2 x 1 - x 2 + 3 z x 2 = - 4 x 2 - z y = 3 x 1 - 2 x 2 + z Qual das matrizes seguintes é incorreta?a) A = 2
Observe o circuito da figura. Determine Z e n t ( s ) Aplique fatores de escala K m = 10eK f = 100 aos elementos. Determine Z e n t ( s )eω o .
Seja v s = 20 cos a t V no circuito da Figura. Determine ω 0 , Q e B , visto pelo capacitor.
Considere os circuitos da F i g u r a14.81 e determine a frequência de ressonância ω 0 , o fator de qualidade Q e a largura de banda B .
Um circuito ressonante em paralelo tem resistência de 2k Ω e frequências de meia potência de 86k H z e 90k H z . Determine:(a) A capacitância.(b) A indutância.(c) A frequência de ressonância.(d) A lar