Numa avenida longa, os sinais de tráfego são sincronizados de tal forma que os carros, trafegando a uma determinada velocidade, encontram sempre os sinais abertos (verdes). Sabendo que a distância entre os sinais sucessivos (cruzamentos)é de e que o intervalo de tempo entre a abertura de um sinal e a abertura do seguinte é de , com que velocidade devem trafegar os carros para encontrar os sinais sempre abertos?
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, pessoal!!
Aqui ele fala pra gente que tem uma certa distância entre dois cruzamentos com semáforos, e que esses semáforos ficam abertos durante um intervalo de tempo .
E ele perguta pra gente qual a velocidade que o carro deve ter pra percorrer essa distância entre os semáforos em menos se , para pegar os dois sinais abertos!
Beleza?
Passo 2
Então, a velocidade é:
Substituindo os valores:
Beleza?!
Passo 3
Mas olha o problema! Ele quer a velocidade em . Entaõ temos que converter essa grandeza.
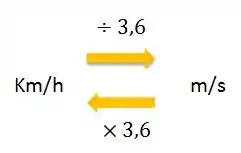
Então, a nossa velocidade fica:
Uhuuul!! Maravilha!
Resposta
Alternativa (d)