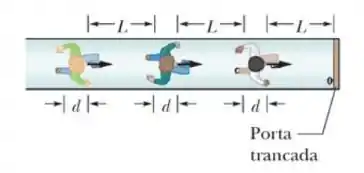
A figura mostra uma situação na qual muitas pessoas tentam escapar por uma porta de emergência que está trancada. A pessoas se aproximam da porta com uma velocidade , têm d = 0,25 m de espessura e estão separadas por uma distância L = 1,75 m. A figura abaixo mostra a posição das pessoas no instante t = 0.
a) Qual a taxa média de aumento da camada de pessoas que se comprimem contra a porta?
b) Em que instante a espessura da camada chega a D = 5,0 m?
Passo 1
Bora pra mais umaaaa!
Cara, o que você precisa perceber nessa questão não é nada mais nada menos que isso:
Se a pessoa se move uma distância com uma velocidade , temos que:
Então, o tempo que cada pessoa leva pra percorrer L com essa velocidade é
E pelo enunciado da questão, a gente viu que com cada pessoa adicional, a profundidade da camada aumenta a profundidade de um corpo sse liga só no esquema onde os bloquinhos coloridos são as pessoas.
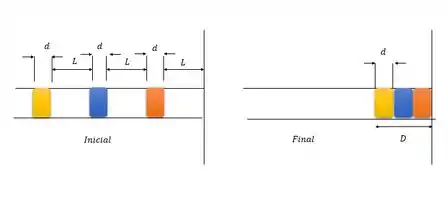
Conforme as pessoas vão chegando na porta a camada vai crescendo. Então, a taxa média de aumento é quanto aumenta essa distância em um determinado tempo. Ou seja, é uma Velocidade Média também, né? :O
Essa é a sacada que cê tem que ter pra resolver essa questão! Então a taxa média vai ser calculada por:
Mas esse tempo aí é o mesmo tempo que a pessoa leva pra percorrer a distância L, que é o tempo de quando alguém anda essa distância e a taxa de pessoas aumenta! Haja coração nessa questão né, ufa.
Então temos:
Substituindo
Substituindo os valores a gente vai ter:
Passo 2
Aqui ficou fácil, né? A gente já tem a velocidade da taxa de aumento e temos o valor de d. Só precisamos jogar na formulinha e descobrir o tempo!
Conseguimos!