A posição de um objeto que se move ao longo de um eixo x é dada por , onde está em metros e em segundos. Determine a posição do objeto para os seguintes valores de :
(a)
(b)
(c)
(d)
(e) Qual o deslocamento do objeto entre e ?
(f) Qual é a velocidade média para o intervalo de tempo de a
(g) Desenhe o gráfico de em função de para e indique como a resposta do item (f) pode ser determinada a partir do gráfico.
Passo 1
Para resolver os item (a), (b), (c) e (d) é bem simples. Temos a equação que nos dá a posição do objeto em função do tempo. Basta substituir os tempos na equação. Fica da seguinte forma:
(a) Para :
Passo 2
(b) Para :
Passo 3
(c) Para t=3s:
Passo 4
(d) Para :
Passo 5
(e) Neste item iremos saber qual foi o deslocamento () do objeto no intervalo de entre e . Como sabemos, a variação () é sempre: variável final – variável inicial.
Por analogia, a equação fornecida pelo exercício ficará da seguinte forma:
é o que queremos calcular.
Sendo assim,
Passo 6
(f) Neste item iremos calcular a velocidade média para o intervalo de tempo de .
Para problemas de velocidade média, a trajetória do objeto não importa! Apenas as posições inicial e final.
Da letra (b) tiramos a posição inicial do móvel () que é de .
Da letra (d) tiramos a posição final do móvel () que é de .
Assim,
Passo 7
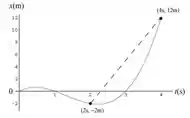
(g) Neste item iremos esboçar o gráfico de em função de no intervalo e indicar a resposta do item (f) no gráfico
Para esboçar o gráfico dessa questão, colocaremos os pontos no eixo cartesiano e vamos verificar como a função se comporta. Pontos já calculados ():
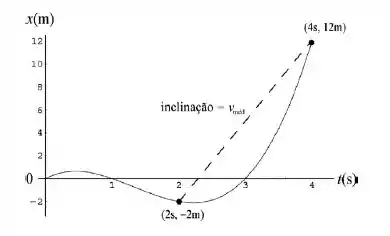
(0,0)
(1,0)
(2,-2)
(3,0)
(4,12)
A reta tracejada que liga o ponto () ao () está representando a velocidade média do objeto entre o intervalo e.
Ufa , acabou rs Bora fazer mais exercícios e garintir a aprovação ??