Um movimento pode ser expresso por vários gráficos de variáveis em função do tempo.

O gráfico da posição X tempo, da velocidade X tempo, da aceleração X tempo e etc...

Os gráficos da posição X tempo e da velocidade média X tempo, no movimento uniforme, são representados por:

(a) Uma reta inclinada ao logo do eixo do tempo e uma reta paralela ao eixo do tempo.

(b) Uma reta com coeficiente angular positivo e uma reta inclinada ao longo do eixo do tempo.

(c) Uma parábola e uma reta inclinada ao longo do eixo do tempo.

(d) Uma reta com coeficiente linear diferente de zero e uma reta com coeficiente angular negativo.

(e) Uma reta com coeficiente angular negativo e uma reta com coeficiente angular positivo.

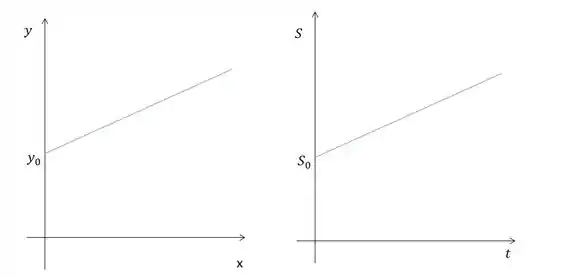
Temos que descobrir como é o gráfico da posição pelo tempo.

Então é o gráfico descrito por essa equação:

Bom, essa e uma equação de primeiro grau (não tem ), e equações de primeiro grau descrevem uma reta, certo?!

Comparando essas duas equações, vemos que a posição é o eixo y, e o tempo é o eixo x. O é o coeficiente angular da reta, que no caso é o valor de , é ele qua dá a inclinação da reta. E o no caso o é o ponto em que a reta corta o eixo , ou

Perfeito?

E em relação a velocidade média?

Bem, se no movimento uniforme a velocidade é contante, então a velocidade média vai ter sempre o mesmo valor. Ou seja:

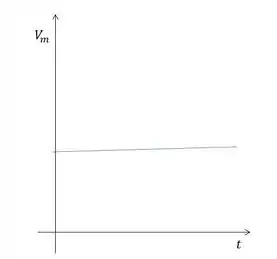
Comparando lá com as nossas alternativas, vemos que a única que descreve esses gráficos que a gente desenhou é a letra (a).