Uma nadadora atravessa um rio com de largura, nadando perpendicularmente à correnteza. Ela chegou à margem oposta em um ponto situado a abaixo do ponto de partida em . Qual é a rapidez média da nadadora em relação à Terra?
(A) 0,50 m/s
(B) 0,80 m/s
(C) 1,20 m/s
(D) 1,30 m/s
(E) 1,40 m/s
Passo 1
Calculando a distância percorrida pela nadadora.
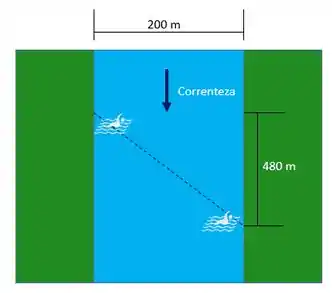
Podemos calcular a distância percorrida pela nadadora utilizando o Teorema de Pitágoras:
Passo 2
Calcularemos a velocidade média.
Para o cálculo da velocidade média, precisamos encontrar o tempo em segundos. Logo:
Calculando a velocidade, teremos:
Resposta
Exercícios de Livros Relacionados
Um vagonete de minério é puxado para o alto de uma encosta a 20k m / h e puxado ladeira abaixo a 35k m / h até a altura inicial. (O tempo gasto para inverter o movimento no alto da encosta é tão peque
A tartaruga começa a corrida 100m à frente de Aquiles. Este corre à velocidade de 10,0m / s , o dobro da velocidade da tartaruga. (A) Quanto tempo Aquiles leva para alcançar a tartaruga? (B) Quanto te
Refaça o exercício 2.1 para o caso (proposto por Zenão) em que Aquiles faz 10m / s e a tartaruga 1m / s .
Considere o caso mais geral do problema de Zenão. As velocidades de Aquiles e da tartaruga são respectivamente, v A e v t e a corrida começa com a tartaruga à distância d à frente de Aquiles. Quanto t
Tomando movimento orbital da Lua em torno da Terra como circular uniforme de raio 3,82 × 10 8m e período de 27,3 dias, calcule a aceleração centrípeta da Lua.