Considere o paralelepípedo em abaixo:
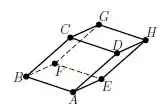
Onde e O volume deste paralelepípedo é:
(a) 15
(b) 16
(c) 17
(d) 18
Passo 1
Se temos 3 vetores e no espaço gerando um paralelepípedo, então o volume do paralelepípedo é dado por:
Vamos escolher os vetores:
Note que, para que eles gerem o paralelepípedo, todos estão com a origem no ponto B!
Passo 2
Então o volume do paralelepípedo gerado pelos 3 vetores vai ser:
Resposta
(b) 16
Exercícios de Livros Relacionados
Calcule a área da superfície de um prisma reto cuja base é um paralelogramo A B C D , com A B - = 6 , A C - = 8 , B C - = 10 e três das arestas verticais têm medidas A A ' - = 2 , B B ' - = 5 , C C '
Mostre que a área do triângulo com vértices x i , y i , para i = 1,2 , 3 é igual à det A 2 , em que A = x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 . (Sugestão: Marque os pontos P 1 = x 1 , y 1 , 1 , P 2 = x 2 ,
Calcule o volume do paralelepípedo que tem um dos vértices no ponto A = 2 , 1 , 6 e os três vértices adjacentes nos pontos B = 4 , 1 , 3 ,C = 1 , 3 , 2eD = 1,2 , 1 .
Calcule a área do paralelogramo em que três vértices consecutivos são A = 1,0 , 1 , B = 2,1 , 3 eC = 3,2 , 4 .
Mostre que o argumento usado no texto para calcular a área de um paralelepípedo pode ser empregado para obter a área de um paralelogramo, diretamente, sem usar o resultado da Seção 10.