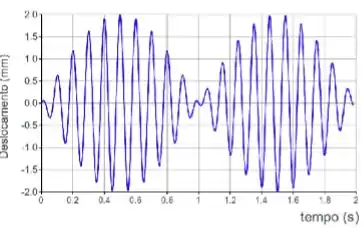
A figura abaixo representa a onda detectada por um microfone posicionado a uma distância qualquer. Sabe-se que esta onda é gerada pela superposição de ondas sonoras senoidais
A seguir marque sempre uma ou mais resposta por item.
Com relação ao padrão de superposição gerado pelas ondas e , se observa que:
A onda resultante apresenta frequência média de e de batimento de
A onda estacionária descrita possui período de .
O gráfico descreve o batimento gerado.
O gráfico descreve a onda estacionária no harmônico.
O gráfico decorre do padrão de interferência construtiva gerado.
Com relação às ondas senoidais e , que compõe a onda resultante exibida no gráfico,
Os valores das frequência angulares são e ou o recíproco e .
O módulo da diferença entre as frequências, , é de
Sabe-se que , já que as ondas se propagam no mesmo meio.
As amplitudes são iguais e valem .
Os valores das amplitudes dependem do tempo.
Passo 1
Vamos entender o gráfico antes: O gráfico mostra o deslocamento que a partícula tem em um determinado intervalo de tempo.
O gráfico apresentado é o tipo de gráfico que representa um batimento, por quê? Bem, porque o gráfico mostra dois momentos um onde a oscilação é rápida e outro momento onde ela é mais lenta. E essa é a situação típica de um batimento. Porque as frequências das ondas sobrepostas são diferentes. Então vamos marcar a alternativa .
A alternativa diz que a frequência de batimento é , isso está errado, porque a frequência de batimento é a frequência do trecho de oscilação lenta, que ocorre em e por isso a frequencia é .
Esse é o trecho de oscilação lenta, pois em um mesmo intervalo de tempo a distancia percorrida pela onda é bem pequena se comparado com outros pontos.
A alternativa e pressupõem que a onda gerada é uma onda estacionária, o que só ocorreria se as frequências de oscilação da onde e fossem iguais e sentido de propagação contrario. O que pelo gráfico vemos que não são por isso geram trechos de oscilação rápida e trecho de oscilação lenta.
A alternativa , o padrão de interferência construtiva é aquele que amplifica todos os ventres e vales da onda, certo? Na figura não vemos isso ocorrendo, tem pontos que foi amplificado, mas também tem pontos que foi reduzido e pontos intermediários. Por isso que temos trechos de diferentes oscilações.
Então a única opção correta é a
Passo 2
Vamos começar pelo que já resolvemos no item anterior.
A alternativa diz que , isso é a definição que demos para você de batimento, que é a diferença entre as frequências de duas ondas sobrepostas. No item anterior vimos que a frequência de batimento é a mesma do trecho de oscilações lentas e por isso vale .
Beleza, a alternativa está correta.
Se a alternativa é correta a alternativa não pode ser correta, pois .
A alternativa diz que porque as ondas se propagam no mesmo meio, o que não é verdade. Pois é:
E é possível termos duas ondas no mesmo material com comprimento de onda diferente, porque o comprimento de onda depende da frequência da onda e da velocidade com que a onda se propaga. Como vimos anteriormente a frequência das ondas são diferentes.
A alternativa diz que as amplitudes são iguais, isso é verdade. Podemos ver que ambas recebem o nome de e não e como ocorre com e .
Mas ela também determina o valor da amplitude sendo . Lembra que falamos que a quando a interferência é construtiva ela iria somar os vales e crista (amplitude). Então se observarmos a imagem a máxima amplitude encontrada é .
E o máximo valor é encontrado quando temos uma interferência construtiva e a amplitude de se soma com a de . Como as amplitudes são iguais e valem . Temos que
O mesmo vale pra interferência destrutiva. Teríamos:
Então é verdade que a amplitude das ondas e valem .
A alternativa cai em contradição com a alternativa , pois se já até encontramos o valor para a amplitude, como que ela pode variar com o tempo? Não rola né, então esta está errada.
Resposta
É correta apenas a alternativa
são corretas as alternativas e