Ao apertar um parafuso cujo centro está no ponto uma pessoa exerce, com a mão direita, uma força de no manete da chave da chave da catraca. Além disso, com a mão esquerda exerce uma força de , como mostrado, para manter o soquete na cabeça do parafuso. Determine o sistema força-binário equivalente em Determine, então, o ponto no plano pelo qual passa a linha de ação da força resultante do torçor.
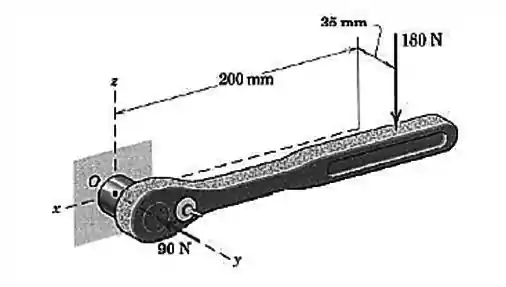
Passo 1
Primeiro vamos escrever a força resultante: perceba que ambas as forças estão indo no sentido negativo de seus respectivos eixos:
Calculando o módulo de , vamos ter que:
Com esses valores, podemos achar o vetor unitário na direção da força resultante:
Então:
Agora podemos escrever a força assim:
Passo 2
Para calcular , perceba que só uma das forças exerce momento em relação ao ponto A linha de ação da força de passa diretamente por , então não tem braço de alavanca.
Assim:
Onde:
Então, o momento será:
Passo 3
Agora vamos usar:
Queremos achar e . Mas sabemos que vetor distância está no plano , então:
Passo 4
Resolvendo :
E terá a mesma direção da força resultante, então:
Passo 5
Então, vamos substituir tudo que achamos:
Mas tudo isso é igual a , né? Então:
Então, vamos igualar os termos de mesma componente e obter as seguintes equações:
Da primeira equa�o temos que:
Da terceira equação temos:
Jogando o valor de que encontramos na segunda equação, vamos ficar com isso aqui:
Assim, o módulo de é dado por:
E para acharmos o vetor , é só multiplicarmos pelo vetor unitário:
E o ponto :