Represente por uma força única em , e por um momento a resultante do sistema de forças atuando em um conjunto de tubos.
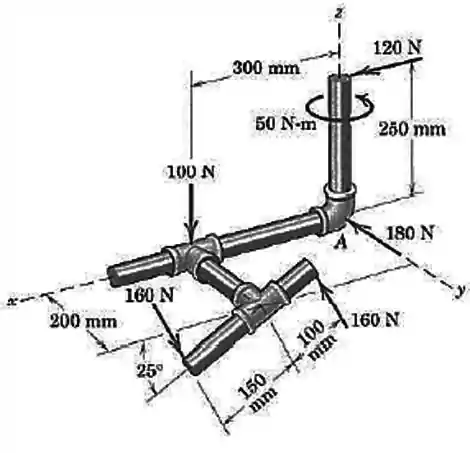
Passo 1
Primeiro vamos determinar a força resultante
Eu sei que existem muitas forças ali o que torna o problema complicado... mas vamos começar descomplicando:
Olhe para as forças de da figura. Percebe que elas têm a mesma direção, mas sentidos contrários?
Isso quer dizer, meu amigo, que a soma delas dá zero. Então não vamos perder o nosso tempo escrevendo essas forças em termos de componente e
Passo 2
Então sobraram as forças de e
Todas elas são paralelas a eixos. Então, olhando para a figura e para o sentido de cada uma:
E é isso!!!
Passo 3
Agora vamos calcular a resultante dos momentos.
De novo em relação às forças de : elas formam um binário, assim o momento delas pode ser representado em qualquer ponto do sistema.
Vamos calcular o módulo do momento delas e definir a direção e sentido pela regra da mão direita:
Pela regra da mão direita:
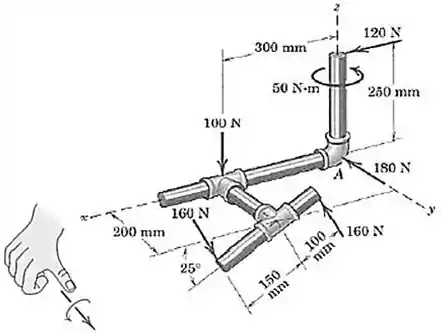
O vetor pode ser escrito por:
Passo 4
Vamos agora analisar a força de : opa, a linha de ação da força passa em cima do ponto . Ou seja, o momento é nulo, pois não terá braço de alavanca:
Falta analisar a força de e a de .
Passo 5
Vamos continuar calculando os momentos e definindo os sentidos usando a regra da mão direita:
Primeiro a força de
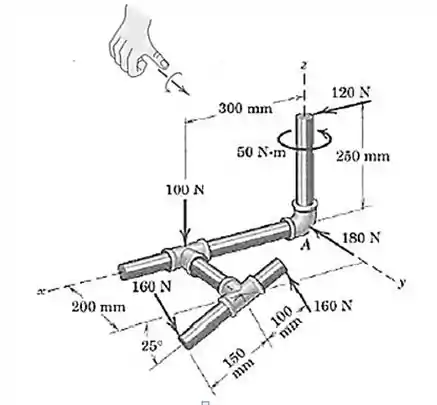
Pela regra da mão direita:
Passo 6
Fazendo a mesma coisa para a força de
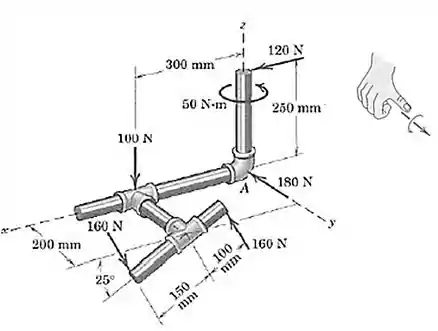
Portanto, o sentido é:
Passo 7
Computamos todos os momentos? Nãaaao, faltou o momento de que já estava aplicado ali como um binário, logo acima do ponto
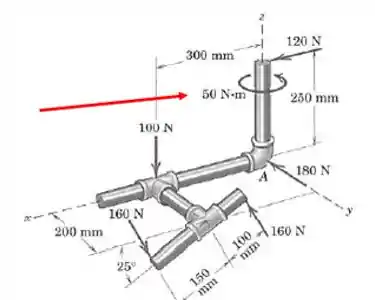
Viu né? Usando a regra da mão direita nele:
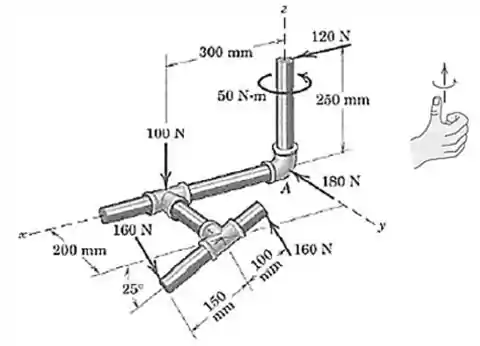
Então o vetor é:
Assim, o momento resultante em relação ao ponto é dado por:
Passo 8
Então, podemos representar o sistema todo no ponto por uma força resultante e por um momento total, dados abaixo: