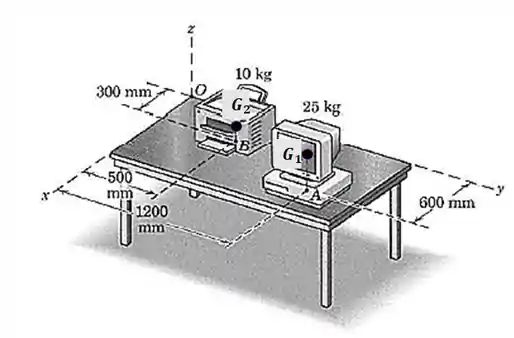
Um computador de e uma impressora a laser de estão sobre o tampo horizontal de uma mesa. Determine a resultante do sistema dos dois pesos correspondentes e especifique as coordenadas do ponto , no plano , pelo qual passa a resultante. Os dois pesos atuam nos pontos

Agora vamos calcular a resultante dos momentos em relação ao ponto

Para isso, vamos antes calcular o vetor de cada um:

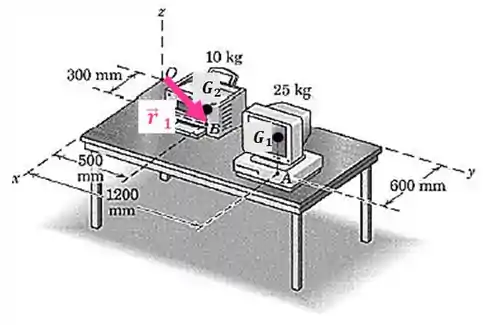
Temos que é o vetor que vai da origem dos eixos até o ponto :

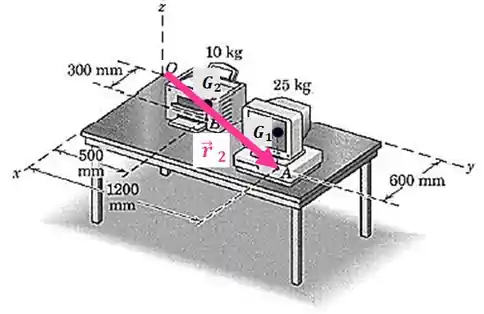
E temos que é o vetor que vai da origem dos eixos até o ponto :

Então:

E para achar , temos:

Então, o momento resultante é:

Para achar o ponto em que passa a resultante das duas forças, vamos ter que achar o vetor tal que:

Por que podemos usar essa relação ao invés da relação que apresenta o vetor momento do torçor? Porque ele é nulo, já que a resultante é perpendicular ao momento resultante:

Nós não sabemos as coordenadas que definem , mas sabemos que ela tem componentes apenas e porque, afinal de contas, todas as forças só atuam no plano .

Assim:

Vamos desenvolver o produto usando essas incógnitas.

Agora, comparando com o momento resultante que tínhamos achado antes:

Igualando componente a componente:

E:

Assim, o ponto onde passa a resultante é: