O avião de passageiros do Prob.2/68 está redesenhado aqui com informações tridimensionais. Se a turbina falha subitamente, determine a resultante dos vetores de empuxo das três turbinas remanescentes, cada um tendo módulo de Especifique as coordenadas e do ponto pelo qual passa a linha de ação da resultante. Esta informação seria crítica para os critérios de projeto de desempenho sob falha de uma turbina.
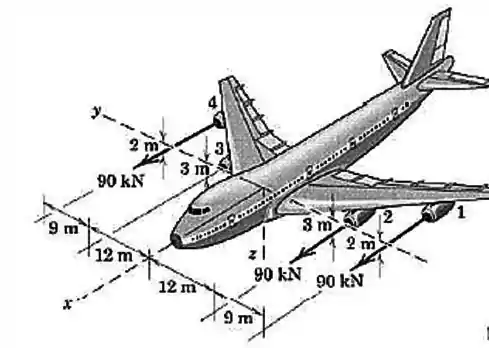
Passo 1
O problema pode ser mais facilmente representado por:
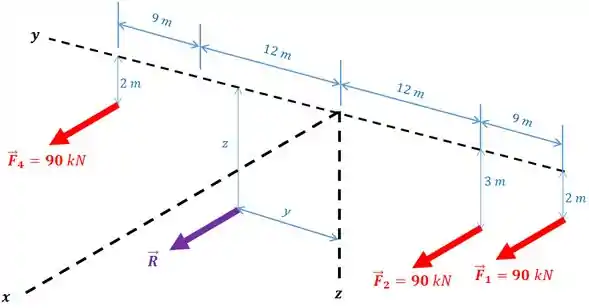
Perceba que todas as forças têm coordenadas Sendo assim, a resultante também terá.
Além disso, veja que o eixo aponta para baixo.
Passo 2
Todas as forças são paralelas ao eixo . Assim, a resultante das forças é dada por:
Passo 3
Agora vamos calcular o momento que cada força exerce no centro do avião. Vamos começar pelas forças da direita:
Turbina 1:
O seu vetor posição é:
Então, vamos fazer o produto vetorial para calcular o momento:
Turbina 2:
O vetor posição é:
Assim, o momento será dado por:
Turbina 4:
O seu vetor posição é:
Perceba que agora o valor de é positivo!
Assim, o momento será dado por:
Passo 4
Pra calcular o momento resultante, vamos somar os três:
Passo 5
Agora vamos descobrir onde a resultante atua, ou seja, o ponto onde ela está aplicada.
Para isso, vamos definir um vetor posição genérico dado por:
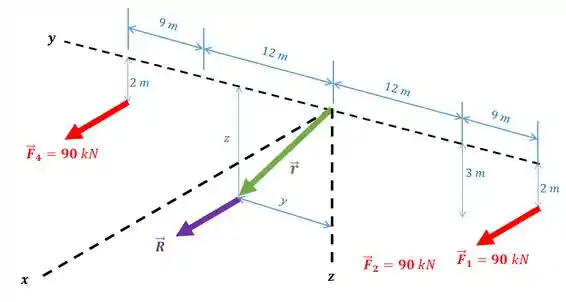
Primeiro vamos ver se o momento resultante é perpendicular à força resultante ou não:
O produto termo a termo dá zero! Assim, podemos dizer que os vetores são perpendiculares.
Então vamos usar a igualdade:
Passo 6
Bora desenvolver o lado esquerdo da equação vista antes:
Desenvolvendo:
Show de bola. Agora só falta comparar com o momento resultante que já tínhamos calculado:
Comparando componente a componente, temos:
E:
Pronto!!!